Surface Morphing

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
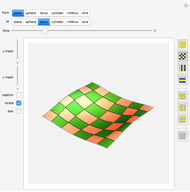
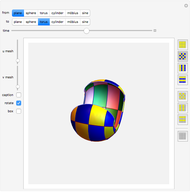
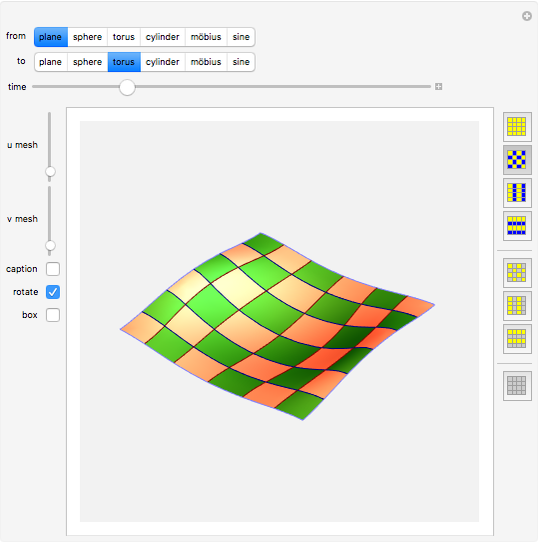
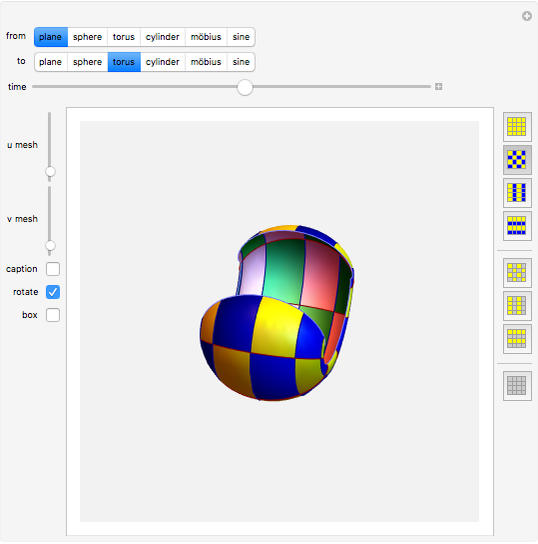
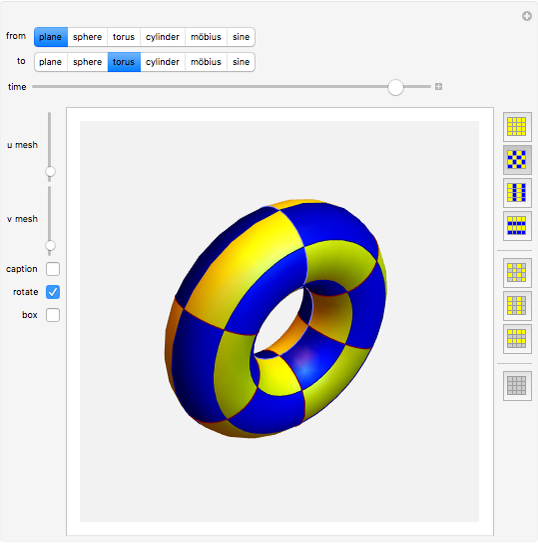
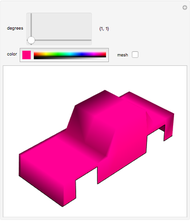
Continuous morphing between two parametric surfaces in 3D.
Contributed by: Yu-Sung Chang (September 2007)
Open content licensed under CC BY-NC-SA
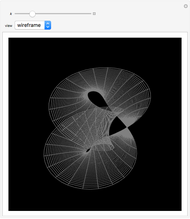
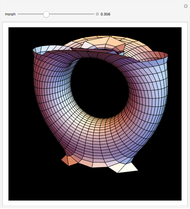
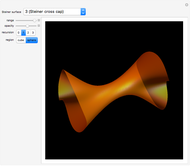
Snapshots
Details
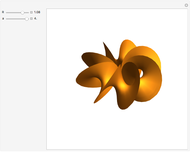
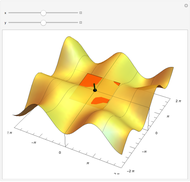
This Demonstration shows morphing between a plane, a sphere, a torus, a cylinder, a Möbius strip, and a sine surface using a continuous transition function.
For any two surfaces which can be defined by continuous parametrizations 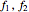 :[
:[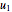 ,
,  ,
, 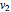 ] →
] → 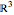 , the transition function can be assigned as: π
, the transition function can be assigned as: π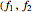 )=(1 - τ(t))
)=(1 - τ(t)) 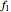 + τ(t)
+ τ(t) 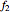 , where τ(t) ϵ [0,1] for ∀t ϵ [0,1].
, where τ(t) ϵ [0,1] for ∀t ϵ [0,1].
Also, we multiply a rotation matrix to the result to provide a 360° view of the morphing.
Permanent Citation
"Surface Morphing"
http://demonstrations.wolfram.com/SurfaceMorphing/
Wolfram Demonstrations Project
Published: September 28 2007