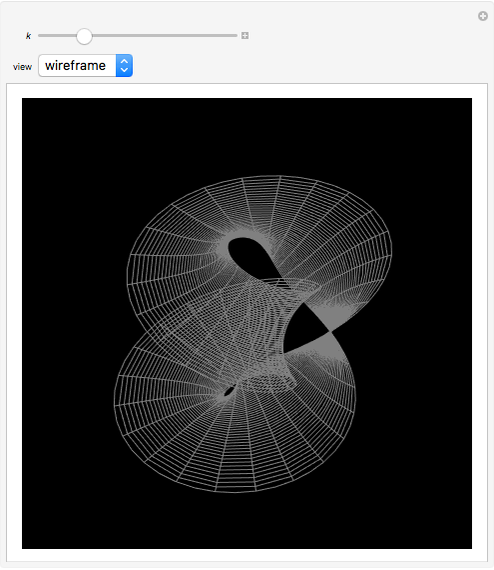
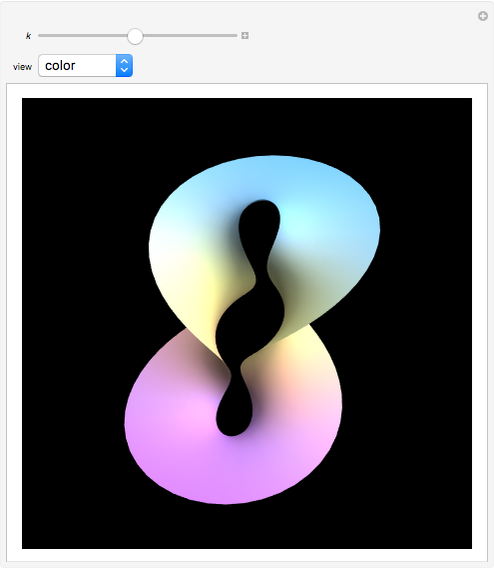
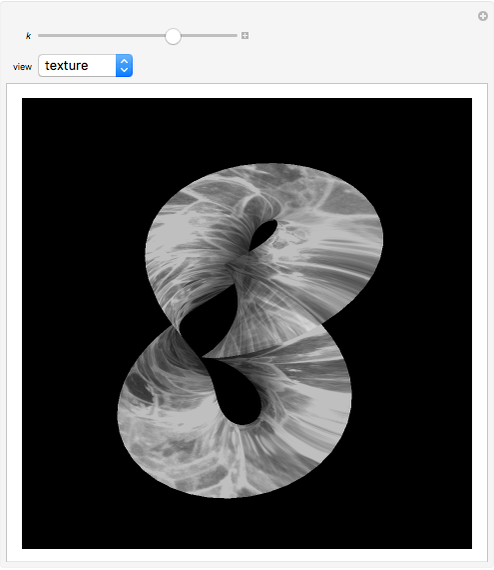
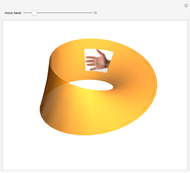
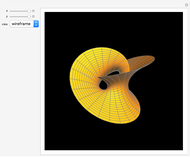
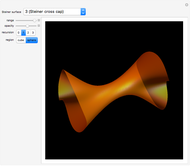
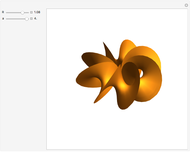
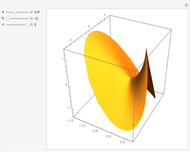
This Demonstration shows a minimal version of the celebrated Möbius strip (a nonorientable surface or one-sided surface). The surface is obtained by computing a Björling curve [1], extrapolating a surface when a determined curve (in this case the circle) is known, along with a given unit normal. The associated surface shown here can be generated by means of a complex conformal transformation, simply by multiplying the minimal curve by the factor 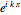[2].