The Interplanetary Magnetic Field (Parker Spiral)

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
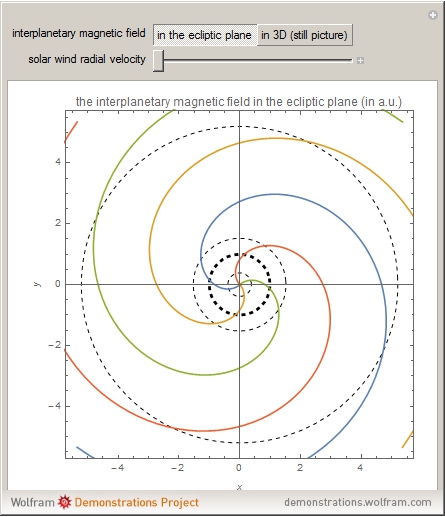
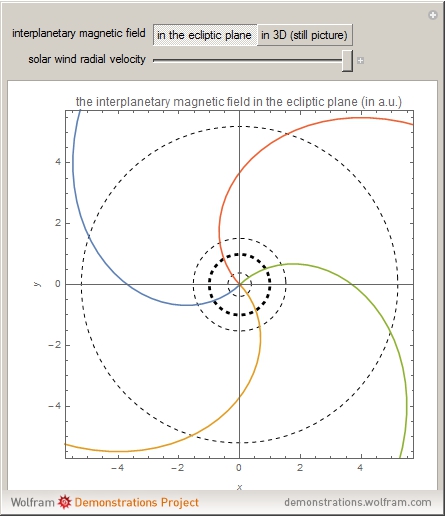
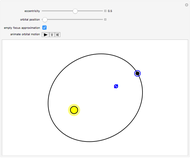
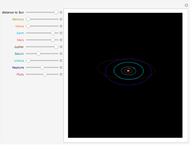
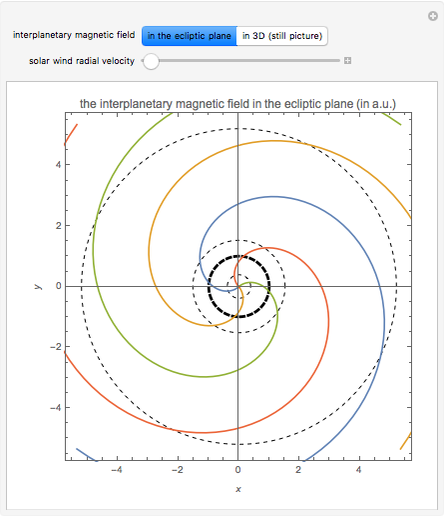
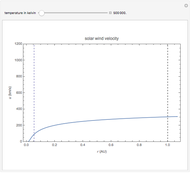
This Demonstration shows the configuration of the interplanetary magnetic field (IMF) that originates in the Sun and is carried into space by the solar wind. The plots are based on the Parker model of the solar wind (see The Solar Wind Demonstration). The Sun's rotation causes the magnetic field streamlines to assume a spiral shape, also known as the Parker spiral. Four arms with different orientation (phase angles) in the ecliptic plane are plotted. You can vary the velocity of the solar wind flow, which is assumed to be constant. Distance is expressed in astronomical units (1 a.u. is the mean distance between the Earth and the Sun). The innermost circle represents the orbit of Mercury. The second, thicker circle represents the Earth's orbit, while the two subsequent circles are the orbits of Mars and Jupiter, respectively. The second image is a 3D plot of the IMF for a radial velocity of 300 km/s.
Contributed by: Ana-Maria Piso (MIT) (February 2009)
Suggested by: Paola Rebusco (MIT), Edmund Bertschinger (MIT), and Michael Louis Stevens (MIT)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Theoretical remarks
The IMF is the magnetic field that originates from the Sun and is convected out into space by the solar wind. The solar wind is composed of ionized particles that move away from the Sun at supersonic speed (see The Solar Wind Demonstration). As the magnetic field lines are entangled in the wind, they are convected outwards with it. We know from observations that, depending on the hemisphere and phase of the solar cycle, the magnetic field spirals inward or outward; the magnetic field follows the same shape of spiral in the northern and southern parts of the heliosphere, but with opposite field direction.
The form of this magnetic field is easy to derive if we make some preliminary assumptions. First of all, we assume steady-state (Parker 1958). Moreover, we assume that the solar gravitation and the acceleration of the solar wind flux can be neglected beyond some distance  , and so we can approximate the outward radial velocity as a constant
, and so we can approximate the outward radial velocity as a constant 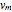 . The tangential component of the velocity,
. The tangential component of the velocity, 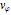 , is given by the Sun's rotation. In ideal magneto-hydrodynamics, we assume that the plasma is a perfect conductor, that is, the interaction between the charged particles can be neglected relative to the much stronger interaction with the magnetic field. This implies that the magnetic field lines move with the plasma—in other words, they are "frozen" into the plasma, and thus the magnetic field streamlines are always parallel to the velocity streamlines.
, is given by the Sun's rotation. In ideal magneto-hydrodynamics, we assume that the plasma is a perfect conductor, that is, the interaction between the charged particles can be neglected relative to the much stronger interaction with the magnetic field. This implies that the magnetic field lines move with the plasma—in other words, they are "frozen" into the plasma, and thus the magnetic field streamlines are always parallel to the velocity streamlines.
For the 2D plot, we restrict the motion to the ecliptic plane and we obtain a differential equation for the radius  and the polar angle
and the polar angle  . The integration of this differential equation gives the equation of the streamlines for the solar wind flow in polar coordinates. The dashed circles represent the orbits of several planets—the thickest one is the Earth orbit at (
. The integration of this differential equation gives the equation of the streamlines for the solar wind flow in polar coordinates. The dashed circles represent the orbits of several planets—the thickest one is the Earth orbit at (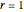 a.u.). To get the 3D plot, we integrate the differential equation for
a.u.). To get the 3D plot, we integrate the differential equation for  and
and  without imposing any restrictions on the angle
without imposing any restrictions on the angle  . We thus obtain the equation of the three-dimensional magnetic field streamlines (in spherical coordinates), for
. We thus obtain the equation of the three-dimensional magnetic field streamlines (in spherical coordinates), for 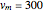 km/s.
km/s.
Mathematical computations
The components of the velocity  are (in spherical coordinates):
are (in spherical coordinates):
 ,
,  ,
, 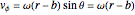
where  is the angular velocity of the Sun and
is the angular velocity of the Sun and 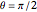 in the ecliptic plane. The field lines are assumed to corotate with the Sun's surface at
in the ecliptic plane. The field lines are assumed to corotate with the Sun's surface at 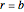 .
.
The differential equation for the velocity streamlines is obtained from  :
:
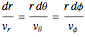 .
.
The equation is integrated from  to
to  and from
and from  to
to  to get:
to get:
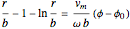 ,
,
the equation of the 3D streamlines for the solar wind. The resulting 3D plot is shown for 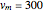 km/s.
km/s.
The dynamic 2D plot shows the two-dimensional spiral in the ecliptic plane.
The gas that flows outwards from the Sun is threaded by the magnetic field lines that originate in the Sun. Because the gas (solar wind) is ionized, it will carry these embedded magnetic field lines with it. Therefore, these assumptions imply that the magnetic field streamlines correspond to the solar wind velocity streamlines.
Conclusions
The resulting plot shows that the IMF streamlines follow an Archimedean spiral, known as the Parker spiral. The Parker spiral is an ideal model—in reality, the radial velocity 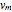 is not a constant, but varies with the distance
is not a constant, but varies with the distance  from the Sun (see The Solar Wind Demonstration). We can model the magnetic field of the Sun as a dipole field,
from the Sun (see The Solar Wind Demonstration). We can model the magnetic field of the Sun as a dipole field, 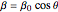 (Parker 1958). This is only an approximation and is valid only at a large distance from the Sun. However, the Parker model is a very good approximation of the magnetic field streamlines and it agrees with observations obtained from various satellites, such as Imp-1 (Wilcox and Ness 1965) or ISEE-1 and ISEE-3 (Russell et al. 1980). The Voyager 1 and 2 probes also confirmed the spiral-like structure of the IMF (e.g. Burlaga 1993).
(Parker 1958). This is only an approximation and is valid only at a large distance from the Sun. However, the Parker model is a very good approximation of the magnetic field streamlines and it agrees with observations obtained from various satellites, such as Imp-1 (Wilcox and Ness 1965) or ISEE-1 and ISEE-3 (Russell et al. 1980). The Voyager 1 and 2 probes also confirmed the spiral-like structure of the IMF (e.g. Burlaga 1993).
References
[1] R. Fitzpatrick, "Flux Freezing," Introduction to Plasma Physics, lecture notes, University of Texas at Austin, 2006 [online].
[2] C. T. Russell, G. L. Siscoe, and E. J. Smith, "Comparison of ISEE-1 and -3 Interplanetary Magnetic Field Observations," Geophys. Res. Lett., 7(5), 1980 pp. 381–384.
[3] J. M. Wilcox and N. F. Ness, "Quasi-Stationary Corotating Structure in the Interplanetary Medium," J. Geophys. Res., 70(23), 1965 pp. 5793–5805.
[4] L. F. Burlaga and N. F. Ness, "Radial and Latitudinal Variations of the Magnetic Field Strength in the Outer Heliosphere," J. Geophys. Res., 98(A3), 1993 pp. 3539–3549.
Permanent Citation