Empty Focus Approximation to Kepler's Second Law

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
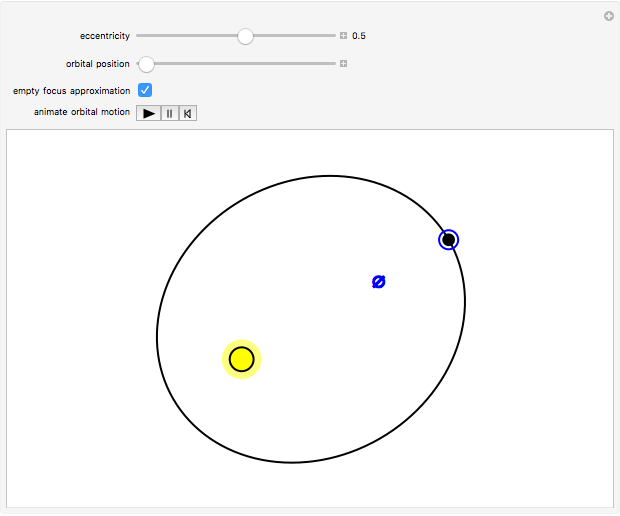
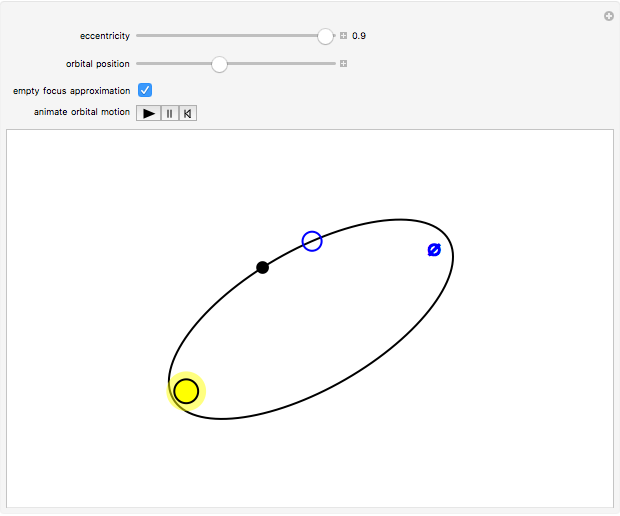
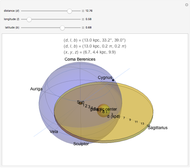
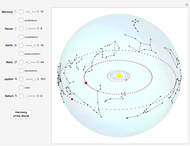
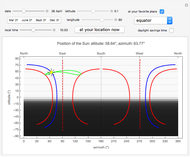
Ptolemy's model for planetary orbits (ca. 150 AD) entails the idea of an "equant" point, a location from which an imaginary observer would see the planet, along with its epicycles, move with an uniform angular velocity. The Ptolemaic worldview was superseded by Kepler's laws of planetary motion (ca. 1605). By Kepler's first law, planets move in elliptical orbits around the Sun at one focus. Kepler's second law implies that the planet sweeps out equal areas during equal intervals of time. This is a consequence of the conservation of angular momentum. The angular velocity about the attracting focus is thus variable, except for a perfectly circular orbit. The planet speeds up around its perihelion (nearest distance) and slows down around its aphelion (farthest distance). There is no mention of the "empty" focus of the ellipse in Kepler's laws. However, the realization that angular motion about the empty focus approximates the equant property was well known to astronomers in the  and
and  centuries.
centuries.
Contributed by: S. M. Blinder (March 2011)
After work by: Jeff Bryant, Stephen Wolfram, and Oleksandr Pavlyk
Open content licensed under CC BY-NC-SA
Snapshots
Details
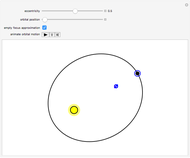
Snapshot 1: the empty-focus construction gives the correct orbital position at aphelion and perihelion
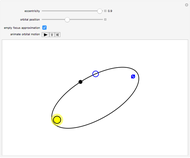
Snapshot 2: it is less accurate for larger eccentricity 
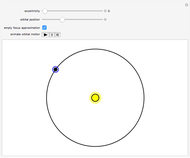
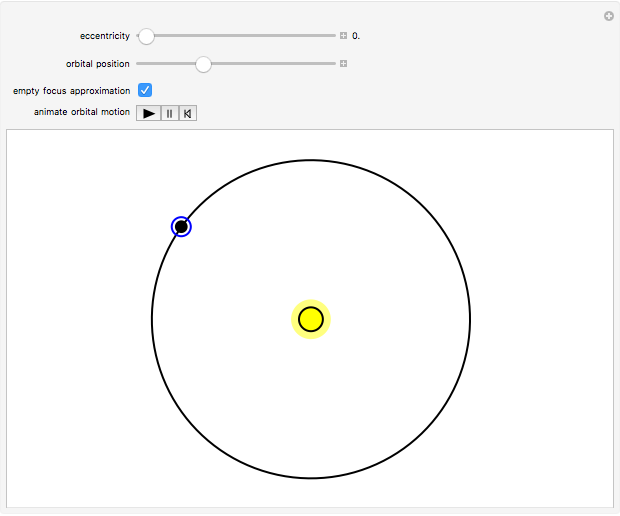
Snapshot 3: but is exact for a circular orbit, with 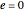
Permanent Citation