Mathematica MathWorld Wolfram Science More »

The Number of Fixed Points in a Random Permutation


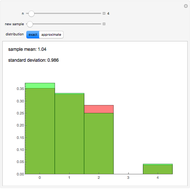
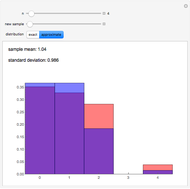
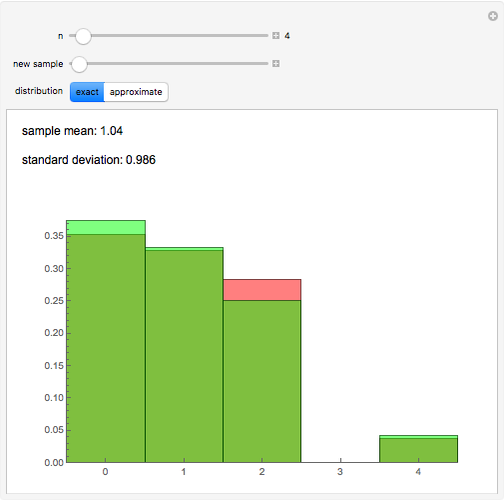
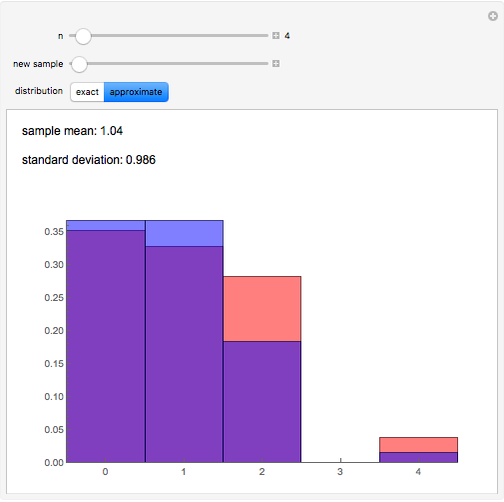
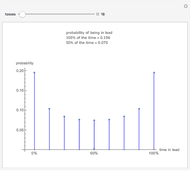
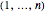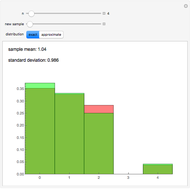
	For a random permutation of , let 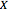be the random variable that counts the number of digits that remain in their original position. This Demonstration allows you to compare the relative frequencies of 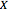obtained in a sample of size 400 with the exact and approximate distributions of 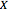. It also gives the sample mean and standard deviation.


	Contributed by: Elcio Lebensztayn

This is the so-called matching problem, in which

individuals mix their hats up and then randomly make a selection. The random variable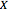

is the number of individuals that select their own hat. The permutations that lead to

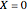are called derangements. The distribution of

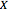is given by

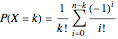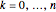. Both the expectation and the variance of

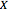equal 1, regardless of the value of

. As

goes to infinity, the distribution of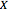

converges to the Poisson distribution with parameter 1.

Report an issue »

	Source page:
	Email	Name (optional)
	Occupation (optional)	Organization (optional)
	I use Mathematica often occasionally never
	Country (optional) Remember me
	Note: Please do not include anything you consider confidential or proprietary. Your message and contact information may be shared with the author of any specific Demonstration for which you give feedback, but will not otherwise be published or distributed. Privacy Policy »

RSS

Atom