The Birthday Problem and Some Generalizations
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
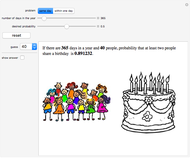
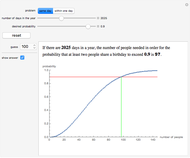
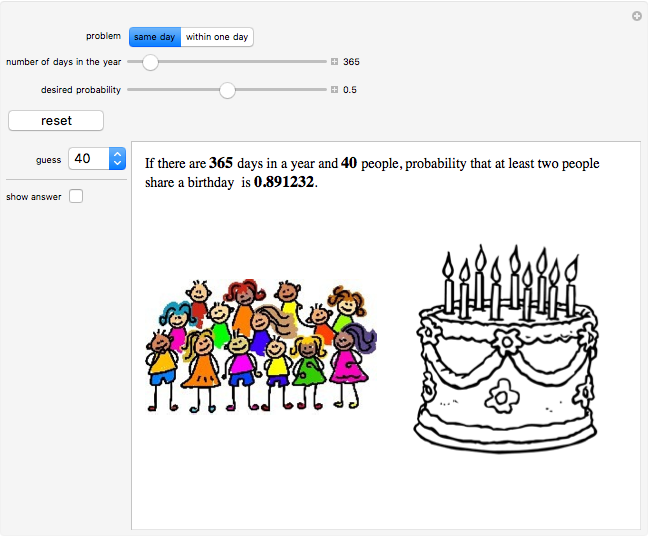
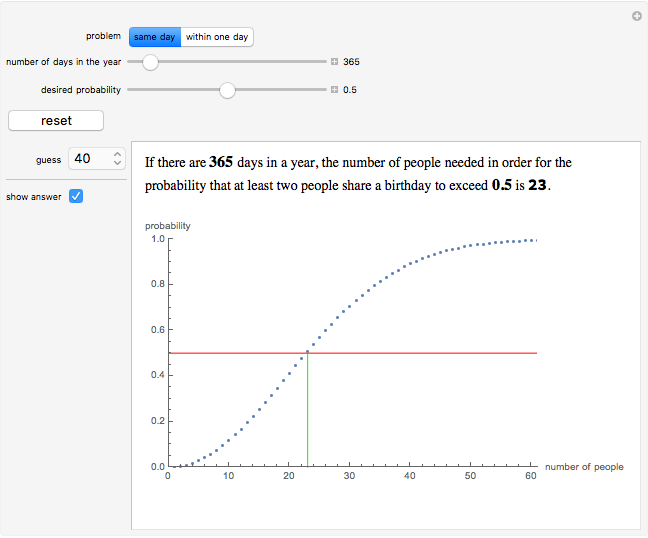
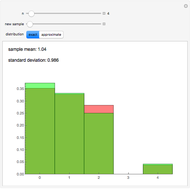
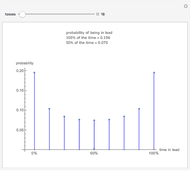
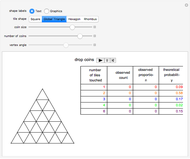
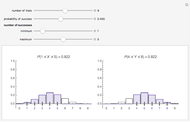
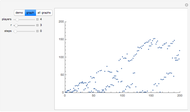
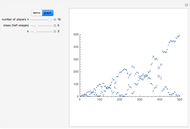
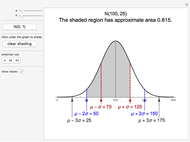
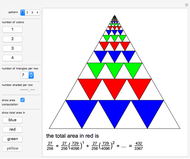
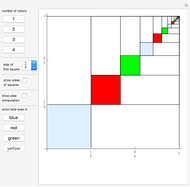
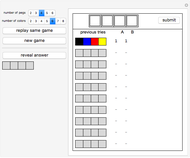
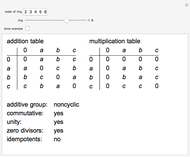
The birthday problem asks, "How many randomly selected people must there be in a room in order for the probability that two people share a birthday to exceed 0.5?" and has the well-known answer 23. The following generalizations are illustrated here, along with answers:
[more]
Contributed by: Marc Brodie (Wheeling Jesuit University) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation