The Secret of Nim

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Explore the mathematical background of the game of Nim and learn how to play the optimal strategy.
Contributed by: Ralf Becker (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
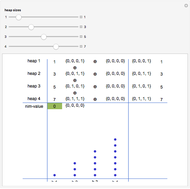
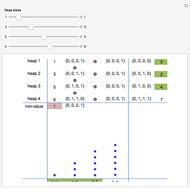
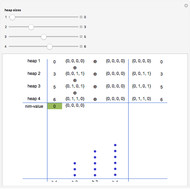
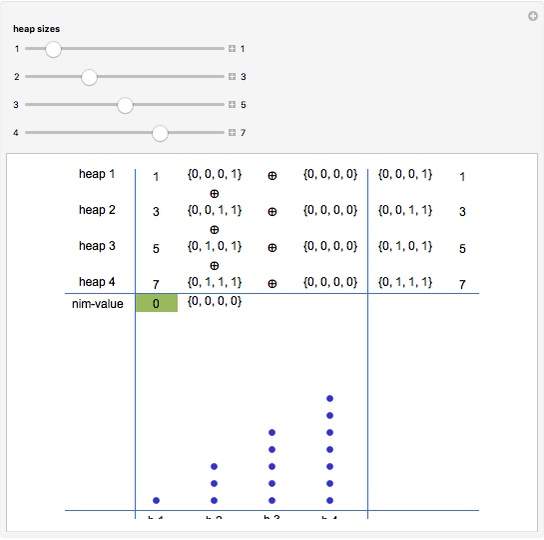
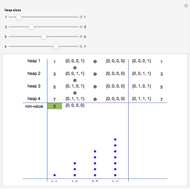
The crucial factor for an optimal (winning) strategy is the nim-value. For details of how to calculate it, see Nim-Value (Wolfram MathWorld). The circle-plus symbol  used in this Demonstration indicates the operation of calculating the nim-value.
used in this Demonstration indicates the operation of calculating the nim-value.
Snapshot 1: if at any point in the game, the nim-value is zero for a given player, the position is safe, which means that player can win with correct play
Snapshot 2: otherwise, the position is unsafe and the player will always lose if the other player plays correctly
Snapshot 3: to achieve a safe position, find a heap  whose size
whose size  is less than the min-value of
is less than the min-value of  with the nim-value of all the heaps; reduce that heap to
with the nim-value of all the heaps; reduce that heap to  , resulting in a nim-value of zero
, resulting in a nim-value of zero
Permanent Citation