Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

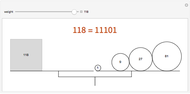
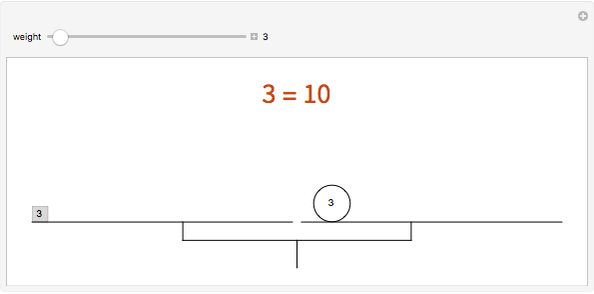
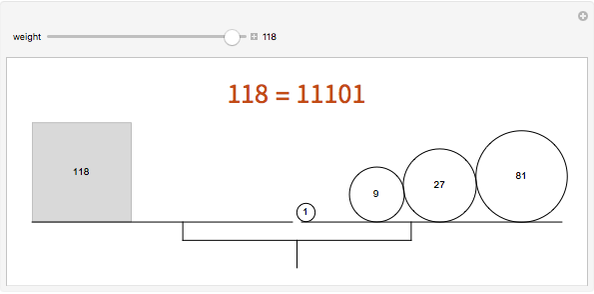
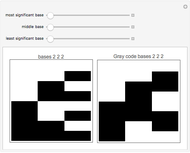
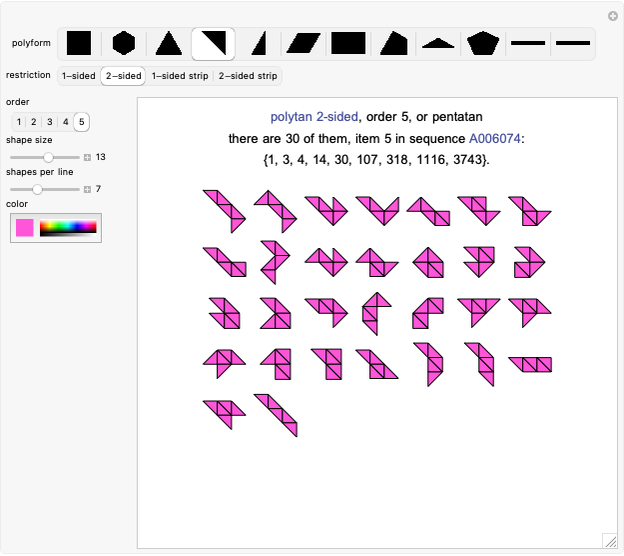
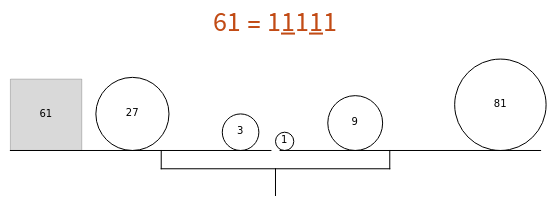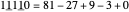Balanced Ternary Notation

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

A number represented in binary is a sum of the powers of 2 (1, 2, 4, 8, 16, ...) multiplied by 0 or 1. For example, 60 in binary notation is , using six "bits".

[more]

Balanced ternary notation multiplies each power of 3 (1, 3, 9, 27, ...) by -1, 0, or 1. In balanced ternary, 60 is , with 1 indicating -1; 60 requires five "trits". With weights 1, 3, 9, 27, and 81, the notation can be used to balance any unit amount from 1 to 121 by putting the weights on either side of the balance pan.

[less]

Contributed by: Ed Pegg Jr (January 2008)
Modified by: Paul Abbott
Open content licensed under CC BY-NC-SA

Snapshots

Details

A nice article on balanced ternary notation is The Balanced Ternary Machines of Soviet Russia by Andrew Buntine.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send