Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Triangles on a Sphere

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

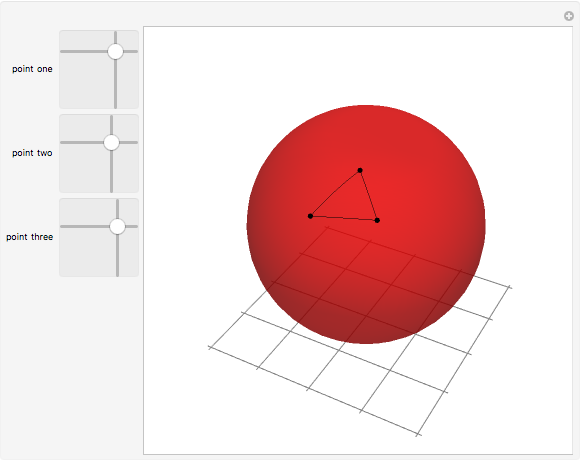
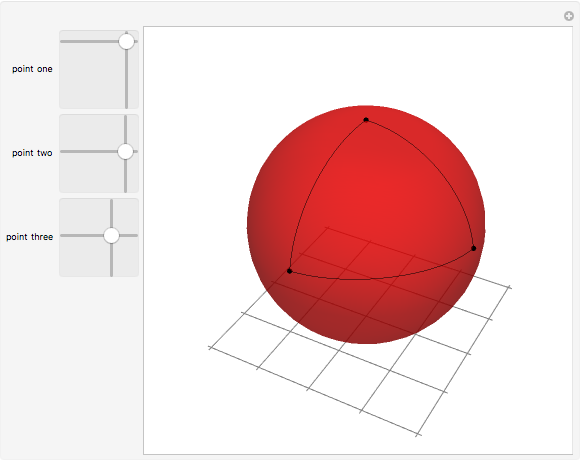
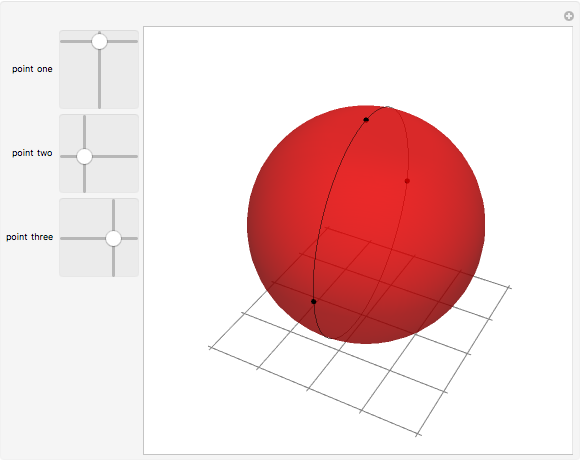
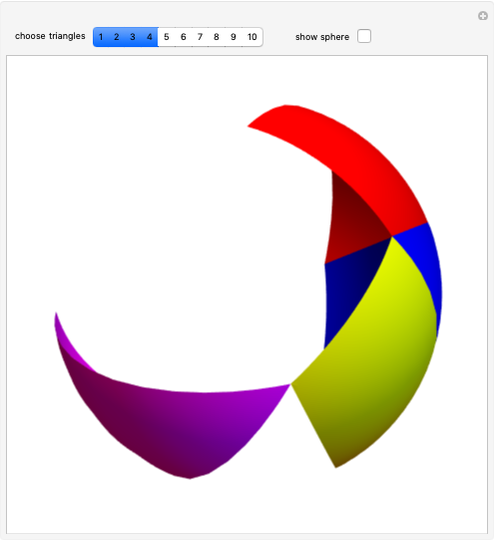
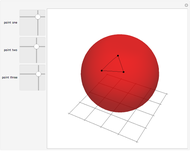
This Demonstration shows a spherical triangle. Three 2D sliders on the left control the vertices with spherical coordinates 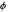and sliding horizontally from 0 to 360° and vertically from 0 to 180°, respectively.

Contributed by: Borut Levart (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

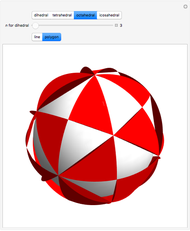
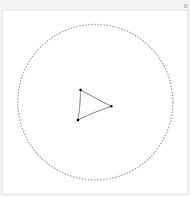
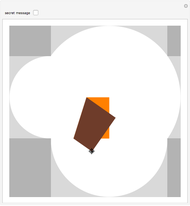
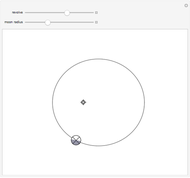
Geometry on a sphere is a noneuclidean geometry. Straight lines are represented as great circles and edges of a spherical triangle are parts of these great circles. The sum of the angles of a spherical triangle is always greater than 180°.

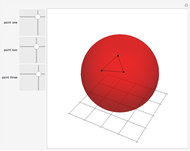
Snapshot 1: vertices close together form a triangle with the sum of its angles close to 180°

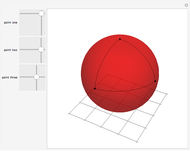
Snapshot 2: a triangle with three right angles, with angle a sum equal to 270°

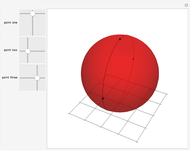
Snapshot 3: all vertices lying on one great circle give an angle sum of 540°

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send