Universal Rhombic Dodecahedron

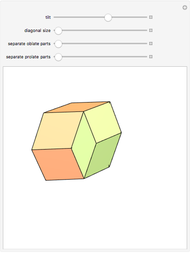
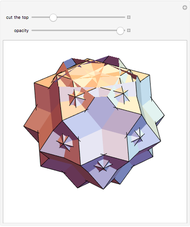
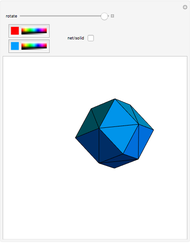
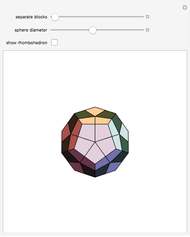
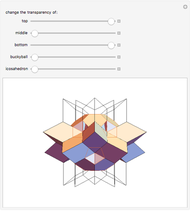
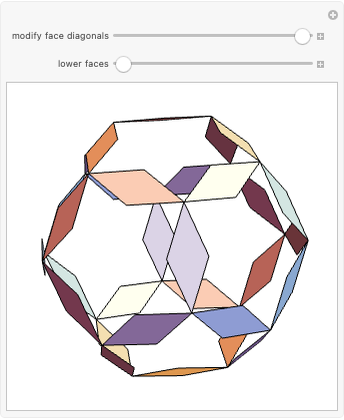
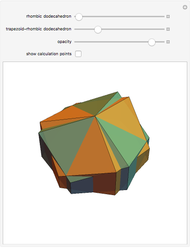
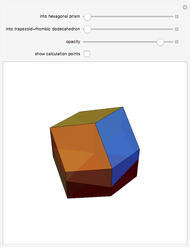
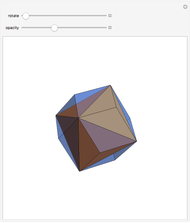
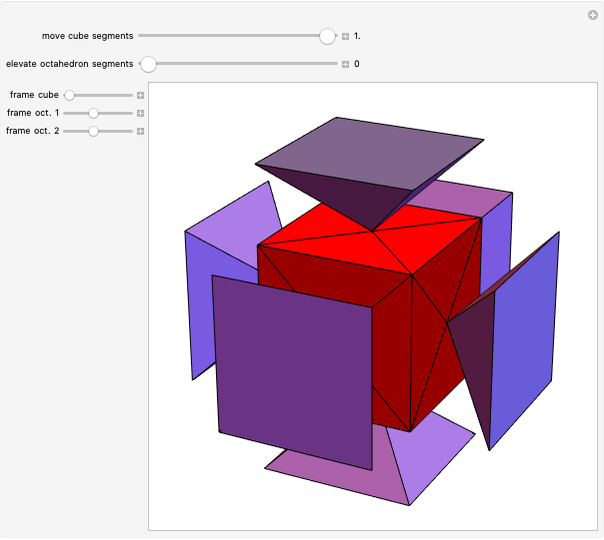
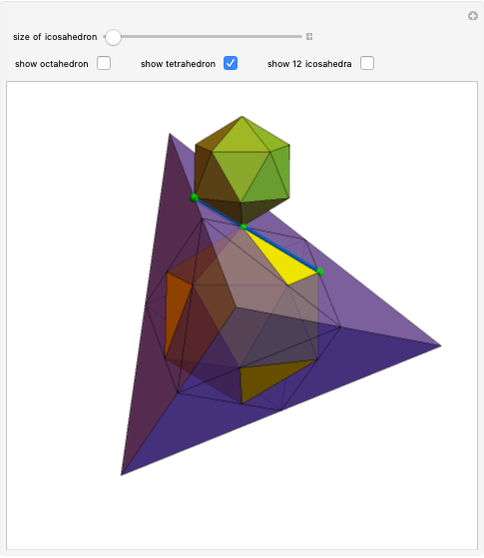
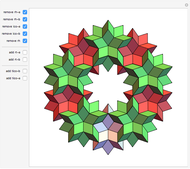
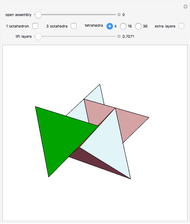
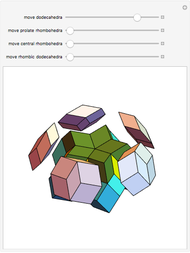
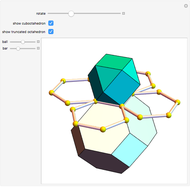
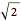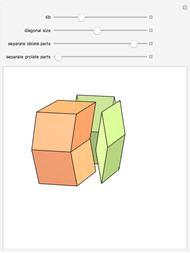
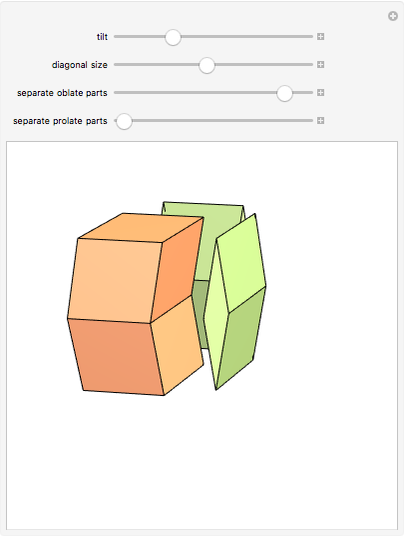
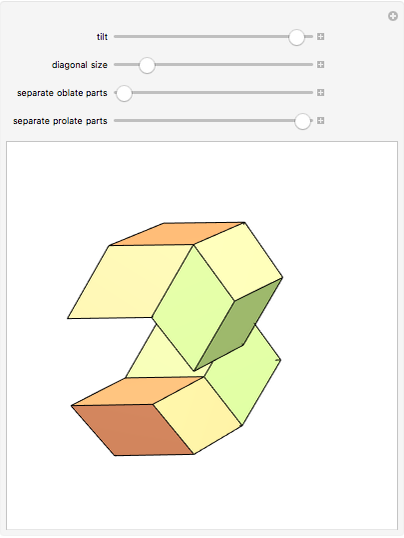
An infinite family of rhombic dodecahedra can be produced by varying the tilt angle of edges and the diagonal of the faces. The possible rhombic dodecahedra include the one having four faces with diagonal ratio and eight faces with diagonal ratio , the rhombic dodecahedron of the second kind (Bilinski) having 12 faces with diagonal ratio , and the rhombic dodacehedron with 12 faces having diagonal ratio 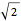. It is also possible to see how the dodecahedra are composed of two oblate and two prolate parts.