Wolfram Demonstrations Project

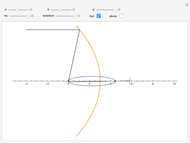
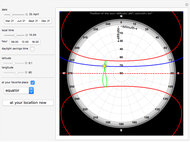
In a horizontal sundial, the angle of the gnomon (the brown triangle) is equal to the latitude

. For a given latitude

, the distribution of the hour-labeled lines is invariant whatever the day of the year; however, sunrise and sunset times change during the year, due to the change in declination.

The sundial is oriented toward North in the Northern Hemisphere and toward South in the Southern Hemisphere.

Enter any location (latitude

°, longitude

°), its standard time zone, the Daylight Saving Time (DST), the date, and solar time (in blue). The result is the shadow angle

, the shadow cast for a 10 cm high vertical pole, the sun altitude

and azimuth

, declination

, sunrise and sunset times, length of day, and local time (in red).

With the knowledge of your latitude

and longitude

, you can build a sundial for your location, using the layout of the hour lines.

Contributed by: Philippe Brosson

Slider Zoom
Gamepad Controls
Automatic Animation

For simplicity, in this Demonstration sunset and sunrise correspond to a solar altitude

, instead of the conventional 50 arc minutes below a horizontal plane.

Latitude

is positive in the Northern Hemisphere and negative in the Southern Hemisphere.

East longitude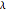

is positive and west longitude

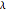is negative.

Examples of time zones: Paris, France +1, New York -4.

Latitudes are limited to be below the Arctic Circle and above the Antarctic Circle;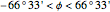

For DST, see Daylight Saving Time.

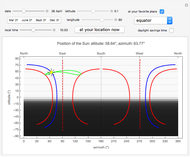
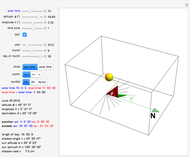
The solar altitude angle

is the angle between the direction of the Sun and a horizontal plane.

The solar azimuth angle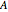

is the angle (measured clockwise on the horizontal plane) from the north-pointing coordinate axis to the projection of the Sun's central ray.

For the definitions of solar altitude angle (

), azimuth angle (

), and declination

The shadow angle

is the angle between the noon line and the shadow cast by the tip of the gnomon.

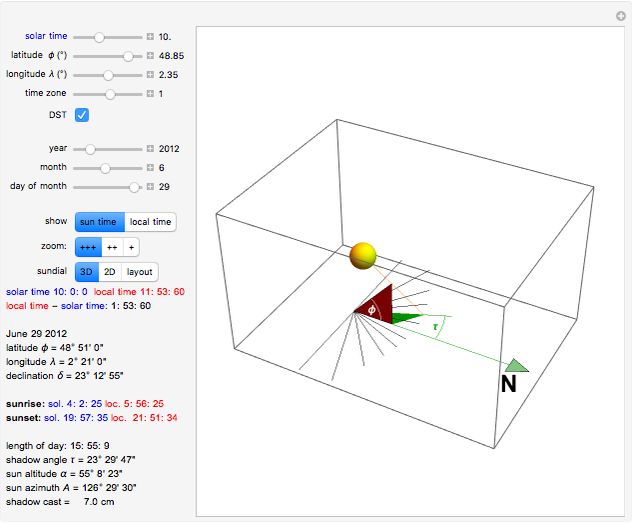
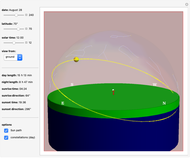
Snapshot 1: 3D view of the sundial in Paris (latitude

, longitude

) on June 29, 2012, standard time zone +1, Daylight Saving Time. The length of day is 15h 55' and the Sun altitude is 55° 8' at 10:00 (solar time).

Snapshot 2: Sundial in Oslo (latitude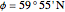

, longitude

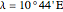) on June 29, 2012, standard time zone +1, Daylight Saving Time. The length of day is 18h 22', which is 2h 27' more than in Paris on the same date.

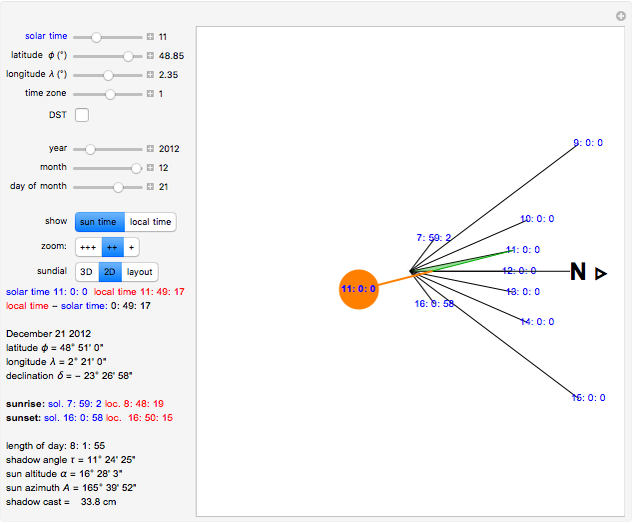
Snapshot 3: Sundial in Paris (latitude

, longitude

) on December 21, 2012, standard time zone +1, no DST. The length of day is only 8h 2' and the Sun altitude is 16° 28' at 11:00 solar time. Even at 11:00 (solar time), the shadow cast is long (33.8 cm for a 10 cm high vertical pole).

Snapshot 4: Sundial in Rio de Janeiro (latitude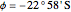

, longitude

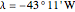) on December 15, 2012 (summer in the Southern Hemisphere), standard time zone

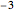, no DST. The length of day is 13h 24' and the Sun altitude is 62° 28' at 10:00 (solar time). The sundial is oriented toward the south.

Snapshot 5: Layout for a sundial in Rio de Janeiro (latitude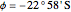

, longitude

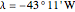) on December 15, 2012 (summer in the Southern Hemisphere), standard time zone

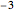, no DST. The length of day is 13h 24' and the Sun altitude is 62° 28' at 10:00 (solar time). The sundial is oriented toward the south.

In Rio, as the date changes from January to December, the day is longest on December 21 and shortest on June 21. The hour lines remain the same (same shadow angles

along the year (except for sunrise and sunset) but they are less in winter than in summer.