Variable States of Polarization Incident on a Wave Plate

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
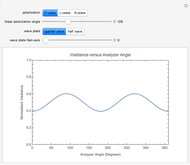
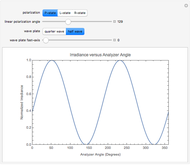
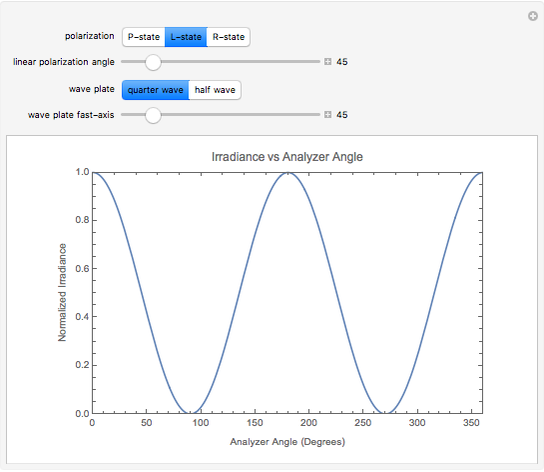
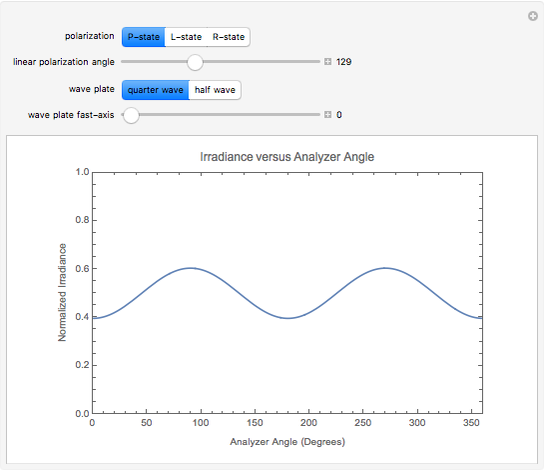
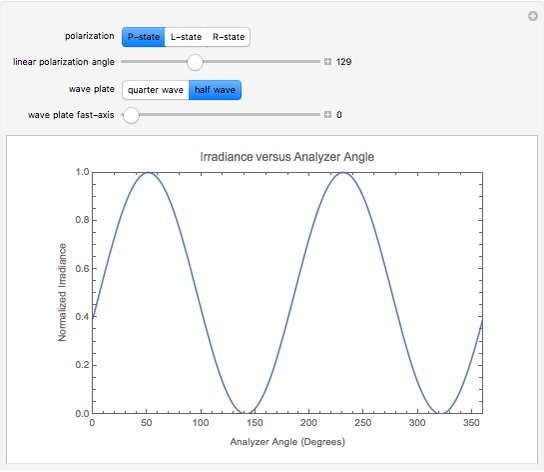
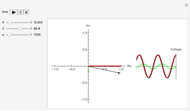
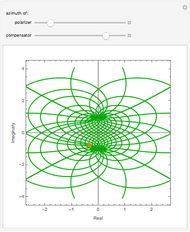
A polarized laser beam passes through a wave plate and then a polarizer. The normalized irradiance is plotted against the analyzer angle. You may choose for the incident polarization to be circular or linear. You may vary the linear polarization angle. You may choose between a quarter- or half-wave plate, and vary the wave plate's fast-axis angle with respect to the  axis.
axis.
Contributed by: Randall J. Hinton (Temple University) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This Demonstration uses a series of Jones matrices and vectors to predict a transmitted wave through a series of optical elements. A Jones vector describes the electric field vector as two scalar components. The phase information is preserved as a complex exponent. When a polarized beam, expressed as a Jones vector, passes through an optical element, it undergoes a transformation that can be expressed as a 2×2 matrix. Each linear optical element has a Jones matrix that describes its transformation of the transmitted wave.
The following equation shows the multiplication of the Jones vector by the polarizer and wave plate Jones matrices;  and
and  are the incident electric field components.
are the incident electric field components.
 , where
, where  is the Jones matrix for the polarizer and
is the Jones matrix for the polarizer and 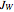 is the Jones matrix for the wave plate.
is the Jones matrix for the wave plate.
The transmitted beam is a vector with components  and
and 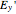 . The irradiance is found by summing the squares of the complex conjugates of each component.
. The irradiance is found by summing the squares of the complex conjugates of each component.
Permanent Citation