Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

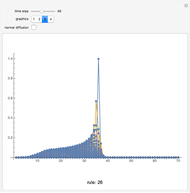
Applying the Iota-Delta Numerical Function to Describe Normal and Anomalous Diffusion Using the Rules 26 and 146

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

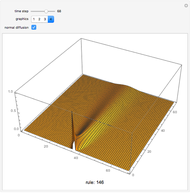
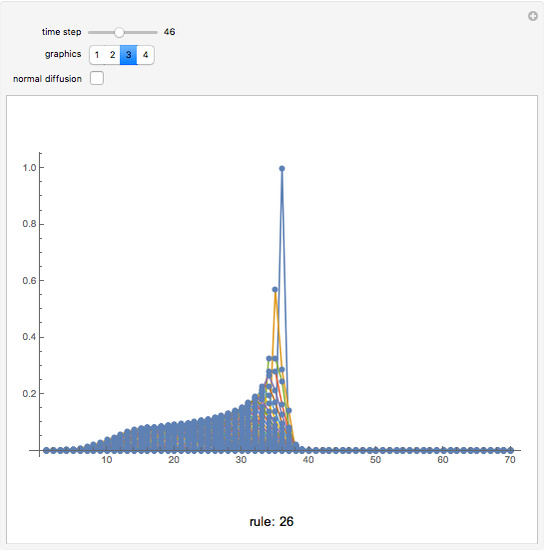
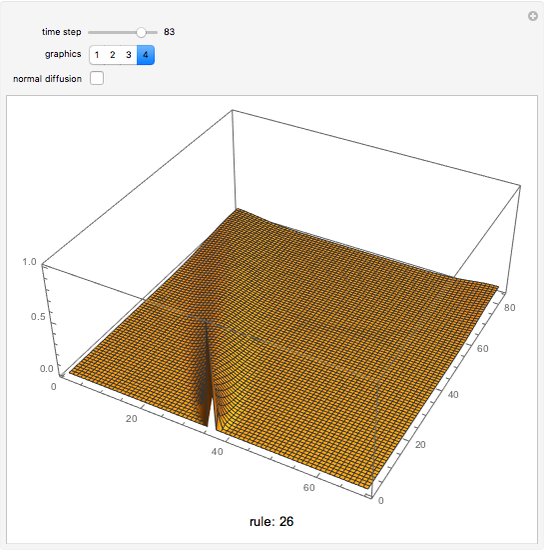
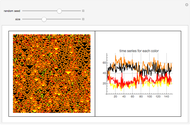
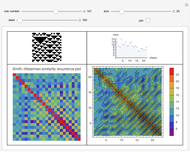
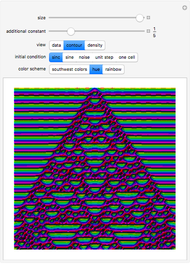
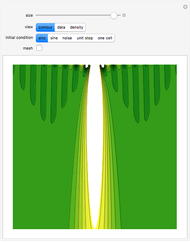
Given the universality of the iota-delta function, we can suppose that it can be used to describe natural phenomena. The description of physical systems can be thought of not only qualitatively (by means of colors) but also numerically by means of taking advantage of the numerical outputs of the function itself. A first point of interest is the control of the sum of the lines. By making a parallel between the iota-delta function and physical systems, if the position in the cellular net is assumed to be a spatial coordinate, the sum of the values of each line of the cellular automaton net is nothing but the amount of a given physical variable in the whole system. In conservative systems, it is clear that the sum of every line must be the same, and we multiply the iota-delta function by a scaling constant . This yields a quantitative interpretation of physical phenomena, as the value of a cell in the cellular automaton net is given as:

[more]

.

It has been proved that when , if is taken as the inverse of the sum of the other coefficients in this equation, a conservative description of a given system is achieved. Also, it has been shown that the iota-delta representation of the elementary cellular automata leads to a straight correlation between it and diffusive-advective phenomena. Besides, the finite difference method, used to solve partial differential equations, has been shown to be a special case of the iota-delta description of a given system.

While considering cellular automata, it is known that different rules generate the same behavior when a unitary initial condition is subjected to both computational systems. When using the scaled iota-delta function representation of a physical phenomenon with the parameters corresponding to two rules that exhibit such similarity of behavior, this ambiguity is immediately broken as the phenomena described by each rule are totally different: one represents the traditional diffusion and the other an anomalous diffusion.

[less]

Snapshots

Details

References

[1] L. C. S. M. Ozelim, A. L. B. Cavalcante, and L. P. F. Borges, "Continuum versus Discrete: A Physically Interpretable General Rule for Cellular Automata by Means of Modular Arithmetic." arxiv.org/ftp/arxiv/papers/1206/1206.2556.pdf.

[2] J.-P. Letourneau, "Statistical Mechanics of Cellular Automata with Memory," M.S. thesis, Department of Physics and Astronomy, University of Calgary, Alberta, Canada, 2006. www.rule146.com/thesis/msc-thesis-letourneau-eca-memory.pdf.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send