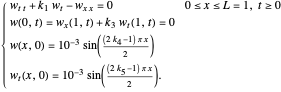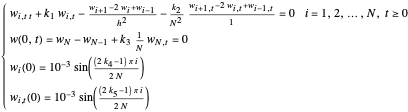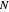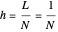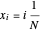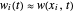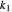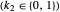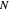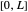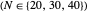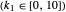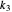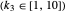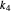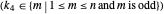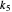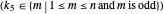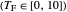Boundary Control of a 1D Wave Equation by the Filtered Finite-Difference Method

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
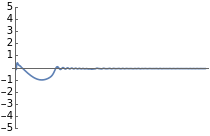
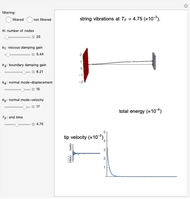
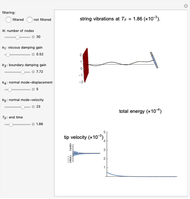
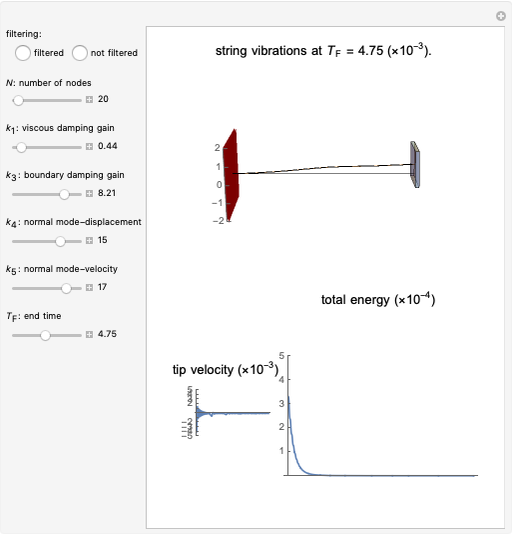
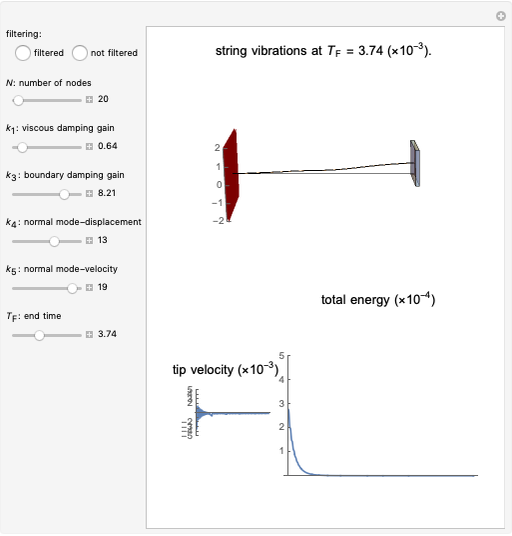
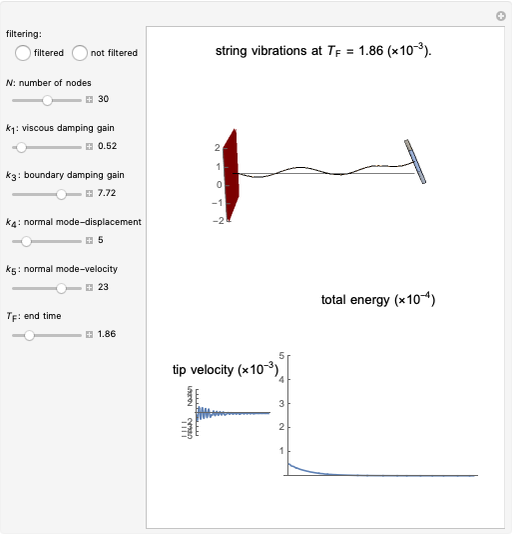
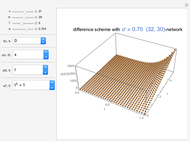
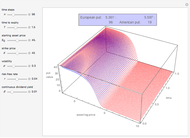
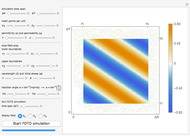
In this Demonstration, the boundary control/stabilization of a wave equation is modeled as a string. The string is clamped on the left and free on the right. The box on the right, used to better visualize the tip displacement and the bending angle of the string, is hypothetical. This box rotates while keeping its normal vector, on the side connected to the string, parallel to the last segment of the string.
[more]
Contributed by: Donald Price, Emma Moore and Ahmet Özkan Özer (June 2020)
Open content licensed under CC BY-NC-SA
Snapshots
Details
In infinite-dimensional control theory, vibrational dynamics are mostly governed by PDEs. To demonstrate the corresponding complex dynamics, model reductions, relying heavily on the finite element or finite difference-based approximations, are unavoidable. For control-free dynamics, these approximations yield reliable and robust results. However, in controlled systems, where the controllers change the dynamics through the boundary of the region, known approximations fail to provide reliable results [1].
This issue is first observed in [1] by considering a boundary-controlled one-dimensional wave equation of a vibrating string of length 1:
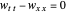 ,
,
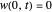 ,
,
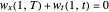 ,
,
 ,
,
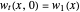
whose solutions are known to be exponentially stable, fails to mimic this behavior as it is approximated by the known approximations, including the finite difference method, finite element method and Galerkin method. Here, the boundary damping term 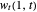 is considered as a state feedback controller.
is considered as a state feedback controller.
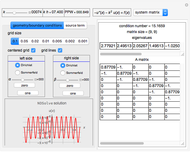
Applying the finite difference method for the PDE above, let the mesh parameter be 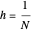 where
where 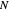 is the number of nodes in the discretization:
is the number of nodes in the discretization:
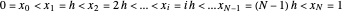 .
.
The approximated solution to 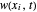 is represented by
is represented by 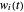 . Therefore the approximated model is:
. Therefore the approximated model is:
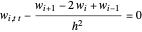 ,
,
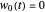 ,
,
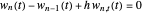 ,
,
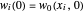 ,
,
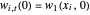 .
.
This problem is handled later by [3], where it is found that the infinitely many eigenvalues of a PDE satisfy a uniform gap condition, whereas the finitely many eigenvalues of the semi-discrete finite difference–approximated model do not. In fact, for high-frequency eigenvalues, the gap between two consecutive eigenvalues approaches zero as the mesh parameter 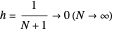 tends to zero:
tends to zero:
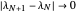 as
as 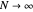 or
or 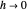 .
.
This is particularly bad for the boundary observability of the high-frequency eigenvalues of the corresponding control-free system, since unobservable systems are uncontrollable [2]. It is simply because the observer cannot distinguish one signal from another.
To remedy this, a filtering technique is proposed in [3]. A viscosity term 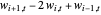 is added to the discretized equation above to obtain:
is added to the discretized equation above to obtain:
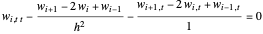 ,
,
 ,
,
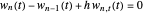 ,
,
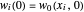 ,
,
 .
.
This convergence of the solutions of the filtered model to the ones of the unfiltered model is shown as the mesh parameter  . The gap condition holds true, and the uniform observability of the filtered model is also shown as the mesh parameter
. The gap condition holds true, and the uniform observability of the filtered model is also shown as the mesh parameter 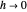 [3]. The same approach is successfully used in [4] for a beam equation where the differential equation is a wave type.
[3]. The same approach is successfully used in [4] for a beam equation where the differential equation is a wave type.
References
[1] H. T. Banks, K. Ito and C. Wang, "Exponentially Stable Approximations of Weakly Damped Wave Equations," Estimation and Control of Distributed Parameter Systems (W. Desch, F. Kappel and K. Kunisch, eds.), Basel: Birkhäuser, 1991 pp. 1–33. doi:10.1007/978-3-0348-6418-3_1.
[2] M. Tucsnak and G. Weiss, Observation and Control for Operator Semigroups, Basel: Birkhauser, 2009.
[3] L. T. Tebou and E. Zuazua, "Uniform Boundary Stabilization of the Finite Difference Space Discretization of the 1-D Wave Equation," Advances in Computational Mathematics, 26(1), 2007 pp. 337–365. doi:10.1007/s10444-004-7629-9.
[4] A. Ö. Özer, "Uniform Boundary Observability of Semi-discrete Finite Difference Approximations of a Rayleigh Beam Equation with Only One Boundary Observation," 2019 IEEE 58th Conference on Decision and Control (CDC), Nice, France, 2019, IEEE, 2019 pp. 7708–7713. doi:10.1109/CDC40024.2019.9028954.
Permanent Citation