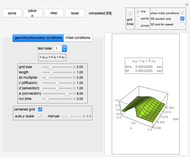
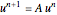Solving the Convection-Diffusion Equation in 1D Using Finite Differences

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
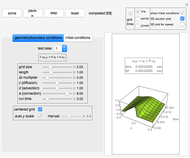
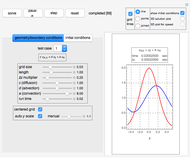
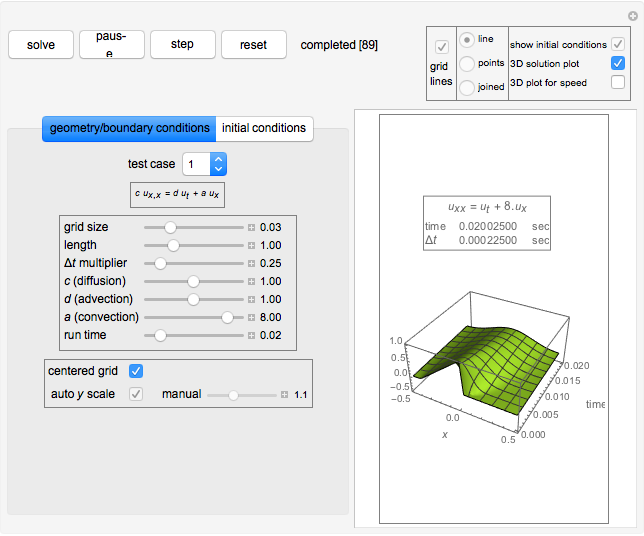
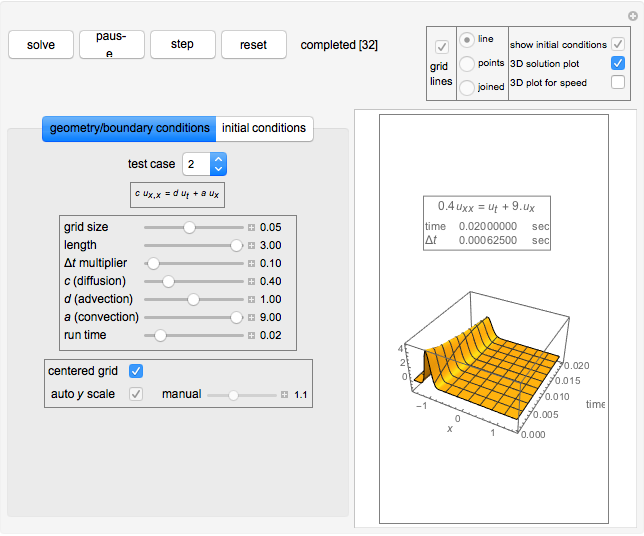
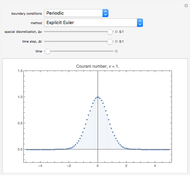
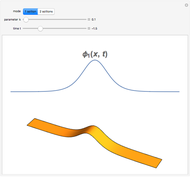
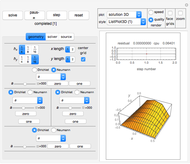
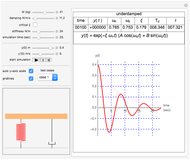
This Demonstration shows the solution of the convection-diffusion partial differential equation (PDE) 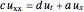 in one dimension with periodic boundary conditions. You can specify different initial conditions. Selected preconfigured test cases are available from the dropdown menu.
in one dimension with periodic boundary conditions. You can specify different initial conditions. Selected preconfigured test cases are available from the dropdown menu.
Contributed by: Nasser M. Abbasi (June 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The convection-diffusion partial differential equation (PDE) solved is 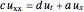 , where
, where  is the diffusion parameter,
is the diffusion parameter,  is the advection parameter (also called the transport parameter), and
is the advection parameter (also called the transport parameter), and  is the convection parameter. The domain is
is the convection parameter. The domain is  with periodic boundary conditions. Initial conditions are given by
with periodic boundary conditions. Initial conditions are given by 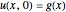 . You can specify
. You can specify 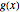 using the initial conditions button. The time step is
using the initial conditions button. The time step is  , where
, where  is the
is the 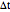 multiplier,
multiplier,  is the grid size, and
is the grid size, and  is the diffusion parameter. You can change the
is the diffusion parameter. You can change the 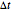 multiplier using the slider. The total run time of the simulation is specified using the slider labeled "time".
multiplier using the slider. The total run time of the simulation is specified using the slider labeled "time".
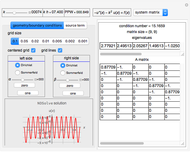
The system solved at each time step is 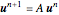 where
where  is the solution of the PDE. The matrix
is the solution of the PDE. The matrix 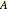 is given by
is given by
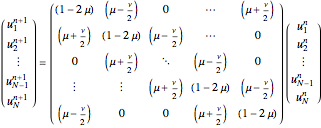 ,
,
where  and
and 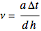 . In the above
. In the above 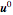 is taken to be the vector of initial conditions. All values used are assumed to be in SI units.
is taken to be the vector of initial conditions. All values used are assumed to be in SI units.
Reference
[1] S. J. Farlow, Partial Differential Equations for Scientists and Engineers, New York: Dover, 1993.
Permanent Citation