Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Center of a Golden Rectangle

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

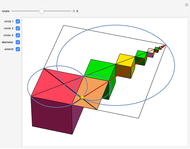
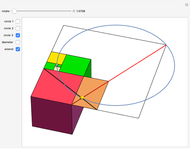
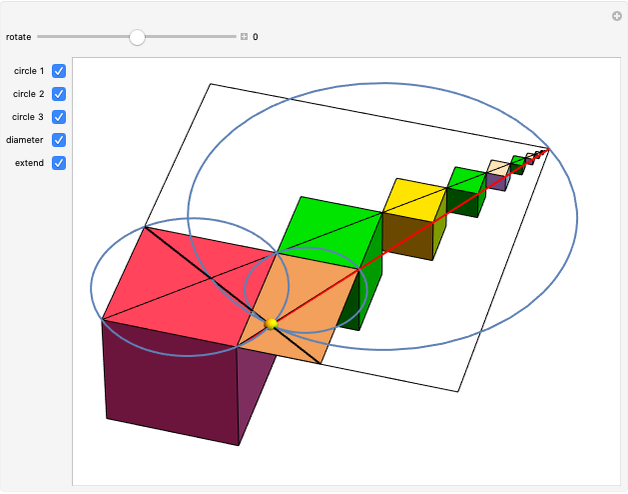
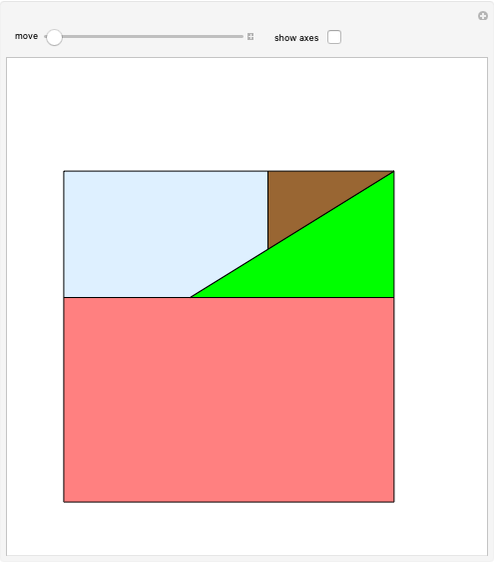
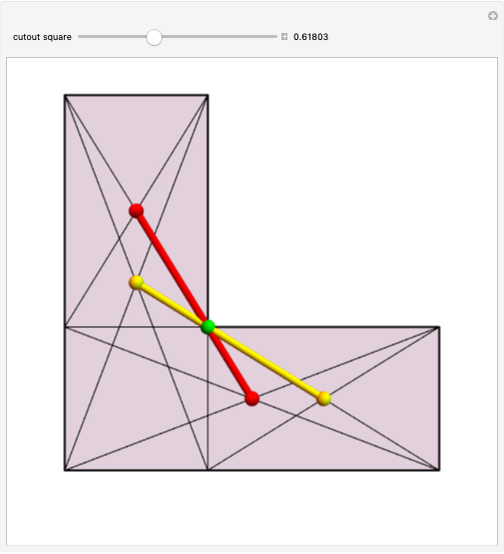
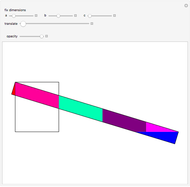
The center of a golden rectangle (GR), shown as the small gold sphere in the figure, is defined as the intersection of the diagonal of a GR formed by a square with a smaller attached GR and the diagonal of the smaller GR.

[more]

The square in is the top face of a cube on which an infinite series of cubes is constructed, connected edge to edge.

Each cube in the series is reduced by (the golden ratio) relative to the previous one.

Suppose the side of the initial cube is 1. The extended red diagonal of the small GR intersects the far vertex of the black square with side . That vertex and the center of the GR are on circle 3, which is traced by the vertex when the series of cubes is folded back into the GR.

The circles placed on the vertices of the squares also pass through the center of the GR.

[less]

Contributed by: Sándor Kabai (February 2020)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send