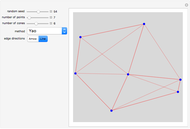
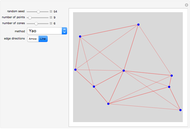
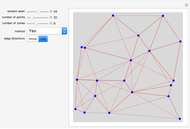
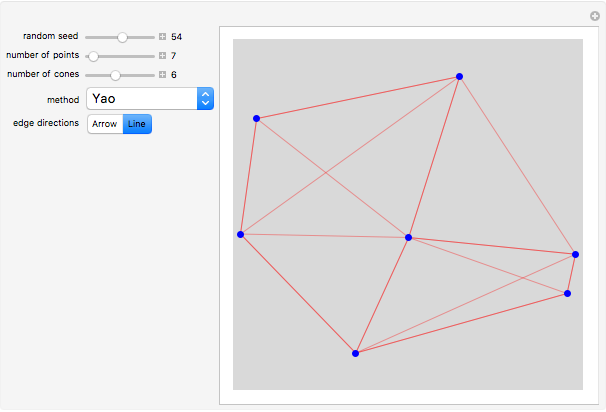
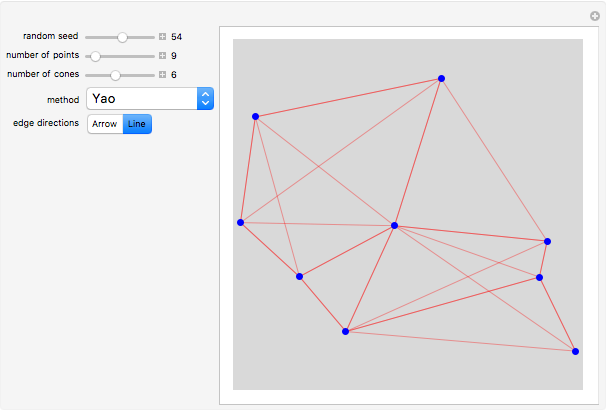
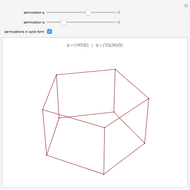
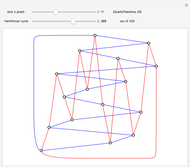
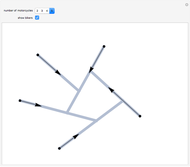
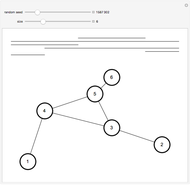
In graph theory, a spanner graph has the property that the length of a shortest path between vertices is no greater than a constant times the spatial distance between the vertices. Cone-based graphs are geometric graphs defined for points in the plane. The space around each point is partitioned into a fixed number of equiangular cones, and a nearest neighbor is selected in each cone. These graphs are known to be spanners for certain values of . Various types of cone-based graphs differ in the way the nearest neighbor is defined.