Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Constrained Optimization: Cobb-Douglas Utility and Interior Solutions Using a Lagrangian

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

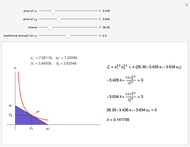
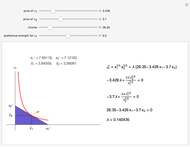
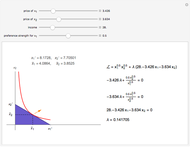
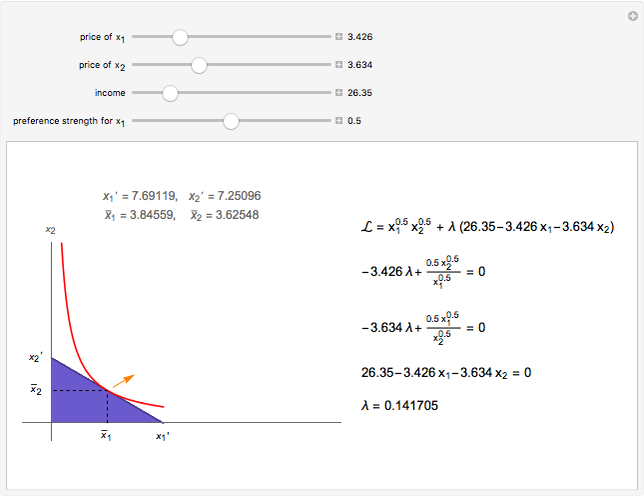
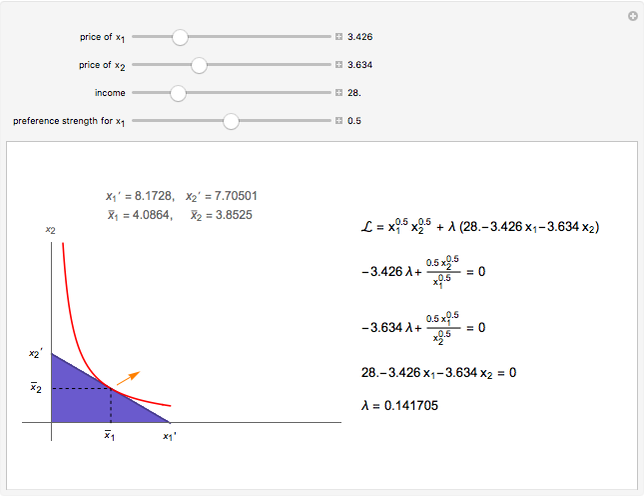
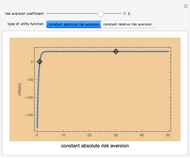
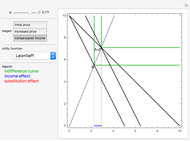
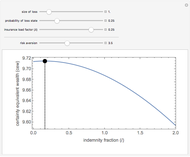
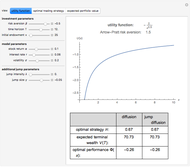
The blue shaded area represents the feasible bundles, those which are on or below the budget constraint, given by the dark violet line. The red curve represents an indifference curve for the individual; the orange arrow indicates the direction of increasing preference.

[more]

This Demonstration is for an individual with Cobb–Douglas utility; it is easily seen that a change in does not affect the optimal amount of , and vice versa. This is peculiar to the Cobb–Douglas utility. Moreover, the solution is always interior.

Mathematically, the right pane shows the Lagrangian followed by the three first-order conditions and the resulting value of the Lagrange multiplier.

[less]

Contributed by: Randy Silvers (September 2012)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The individual's optimal choice is a result of the tension between what is feasible, to the southwest, and what is desirable, to the northeast. Graphically, as long as the individual's indifference curve and budget constraint are not tangent, the individual could improve by trading off one good for the other. Thus, the optimal choice is on the highest indifference curve that has a feasible bundle, at the tangency.

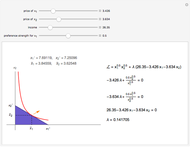
Mathematically, the Lagrangian shows this by equating the marginal utility of increasing with its marginal cost and equating the marginal utility of increasing with its marginal cost. These are the first two first-order conditions. The interpretation of the Lagrange multiplier follows from this. The third first-order condition is the budget constraint.

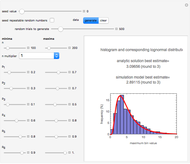
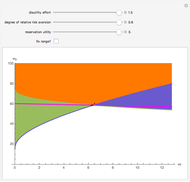
Suggested exercise: Adjust the values of , , , and one at a time, anticipating how the graph will change, and rewriting the Lagrangian and re-solving for the optimal bundle, the value of the Lagrange multiplier, and the resulting optimal utility level; in particular, increase by 1 and note the change in the resulting utility levels.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send