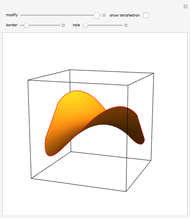
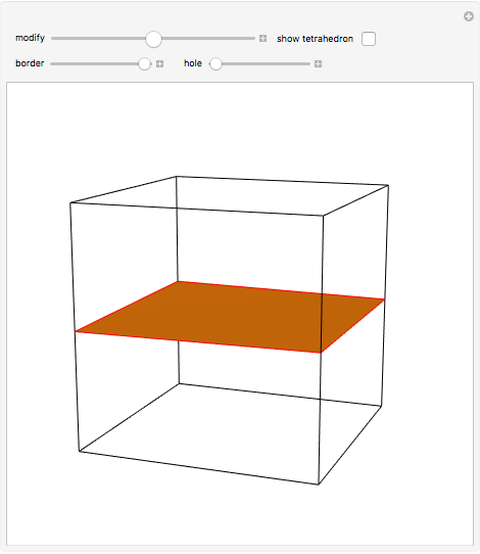
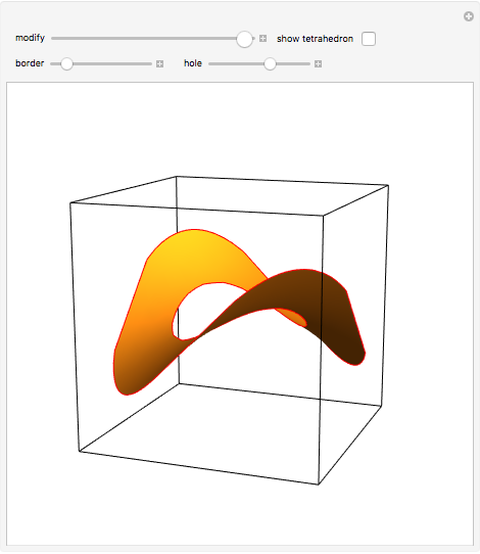
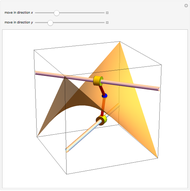
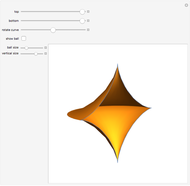
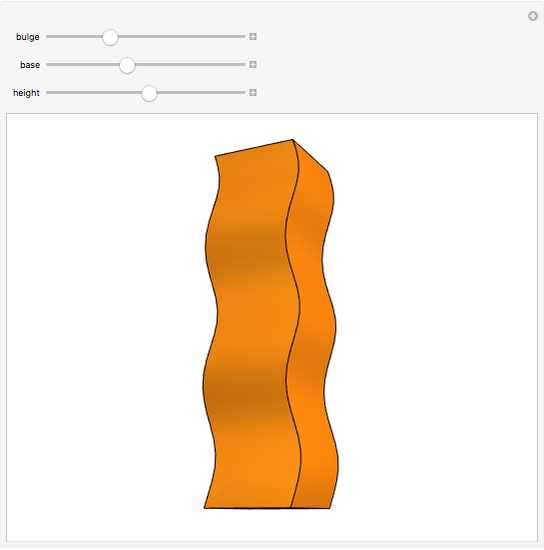
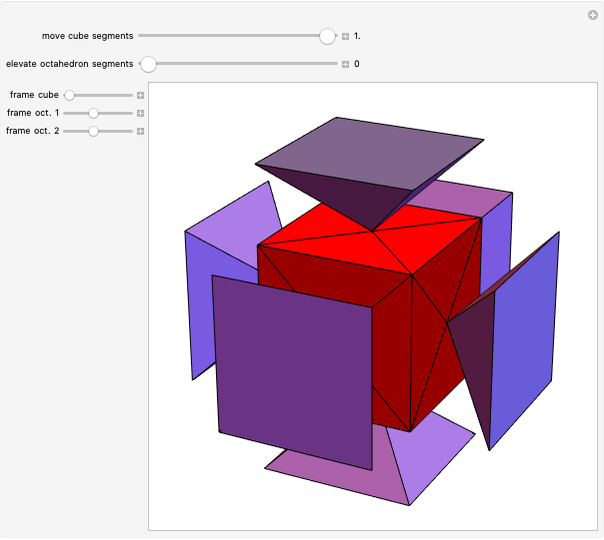
Consider the horizontal square cross section of a cube through its center. Distort the square by moving pairs of opposite vertices vertically along the edges of the cube until they coincide with the vertices of the cube. Each of the intermediate figures is a hyperbolic paraboloid. At either extreme position, the edges form four of the edges of a regular tetrahedron.