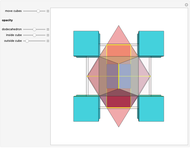
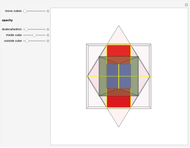
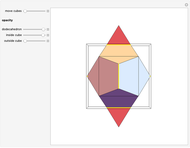
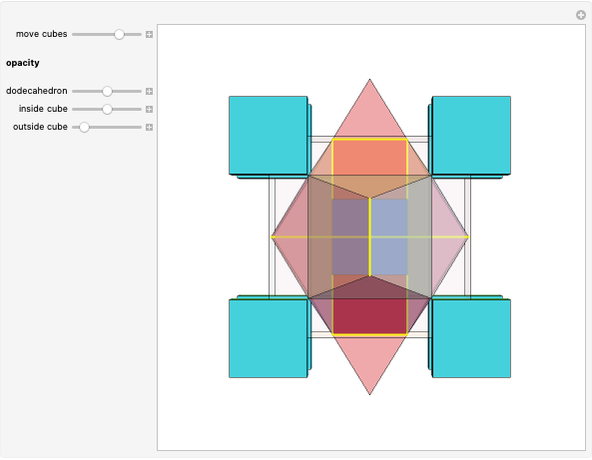
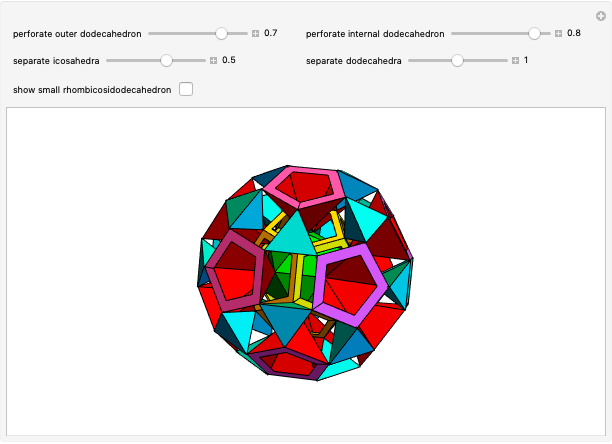
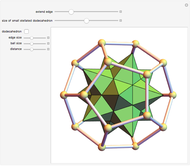
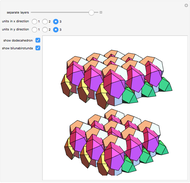
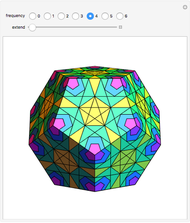
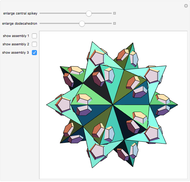
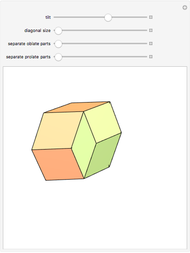
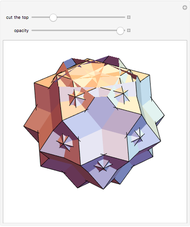
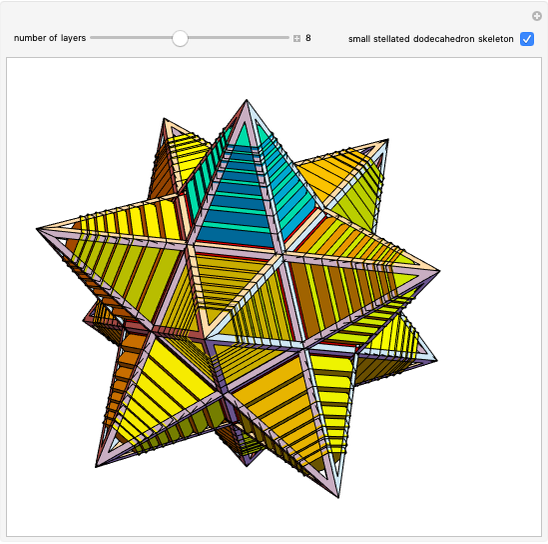
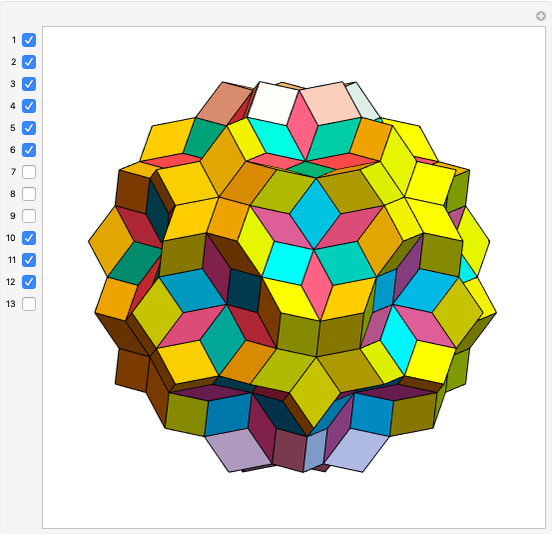
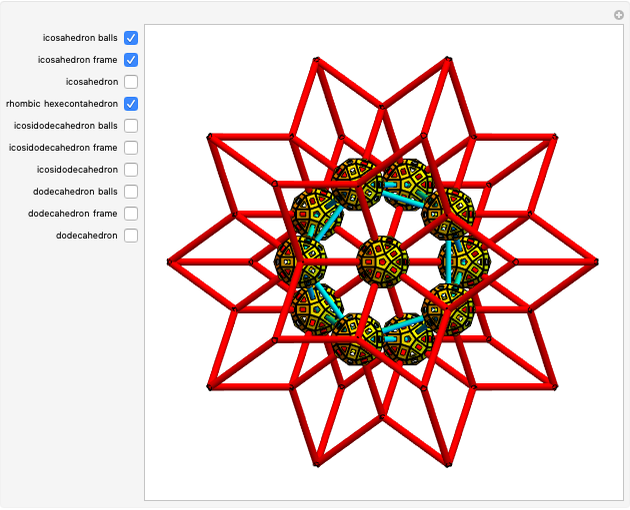
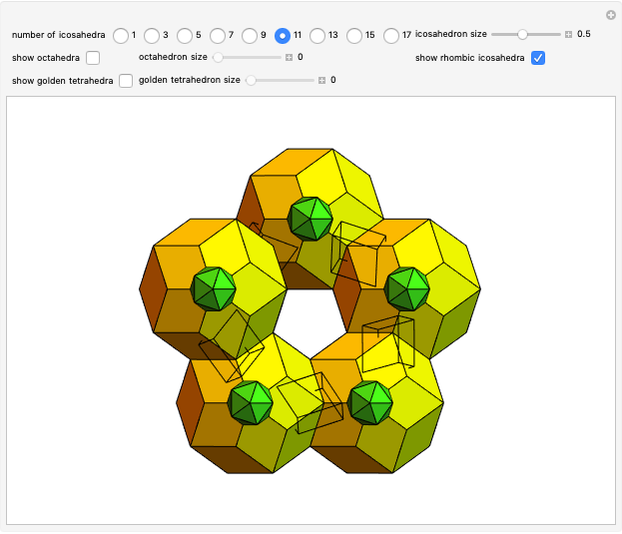
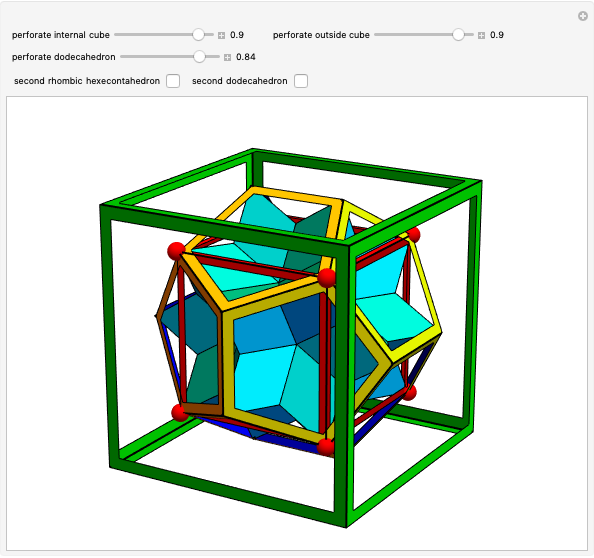
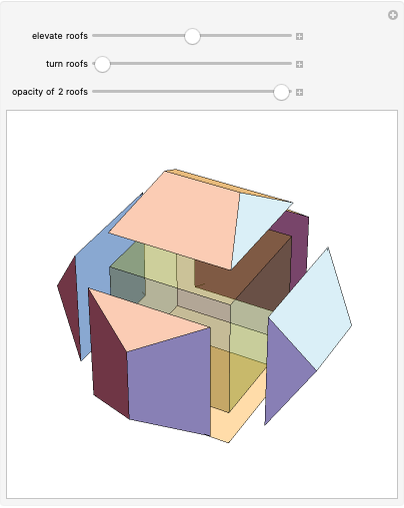
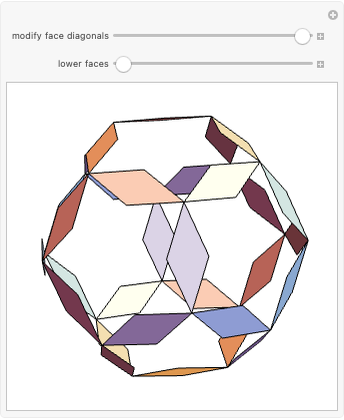
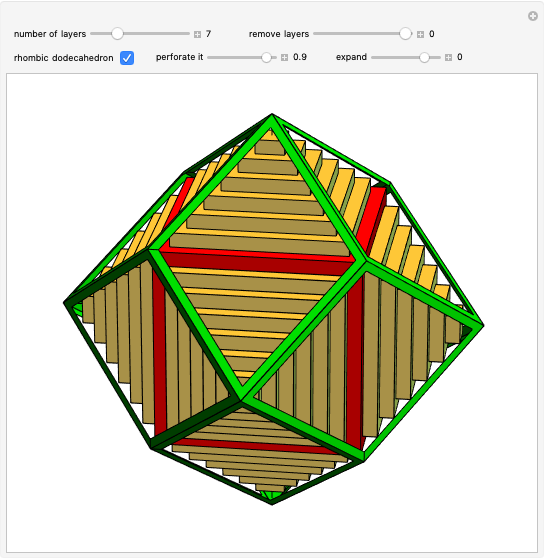
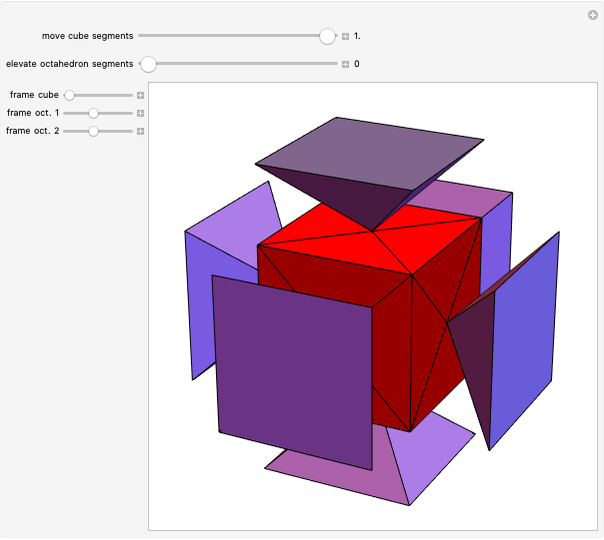
Dodecahedron Measures
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
These facts are enough to reconstruct many of the measures and features of a dodecahedron with edge length one:
[more]
Contributed by: Sándor Kabai (January 2008)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation