Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Driven Damped Oscillator with Resonance Effect

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

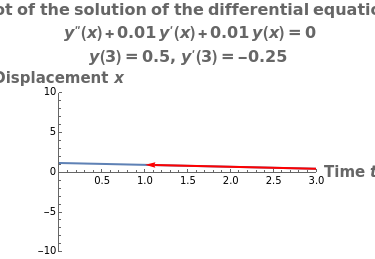
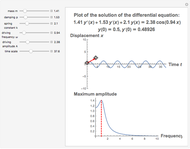
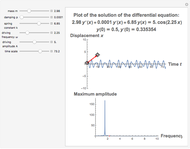
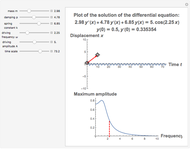
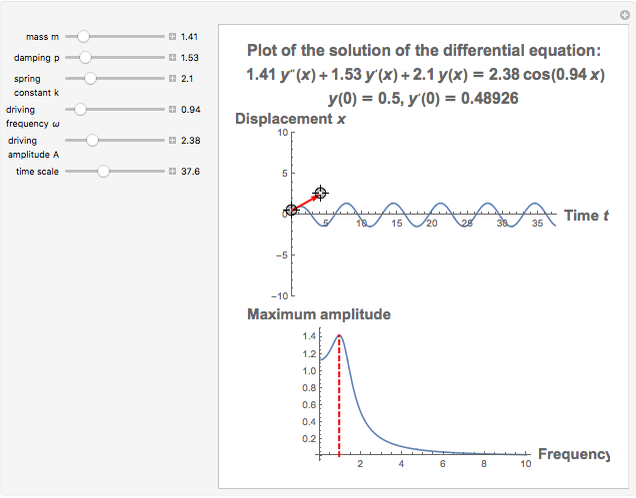
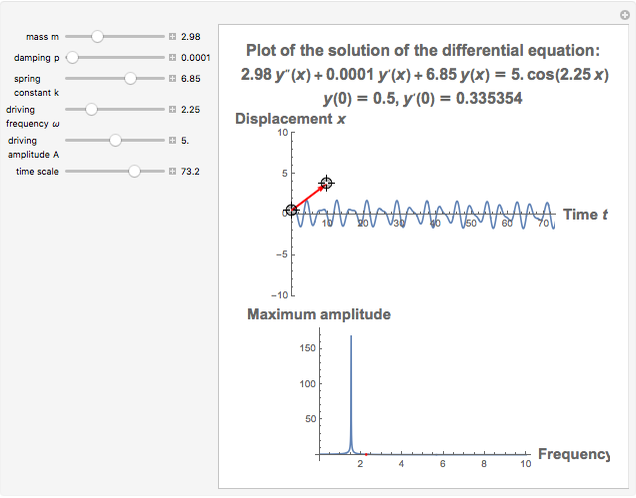
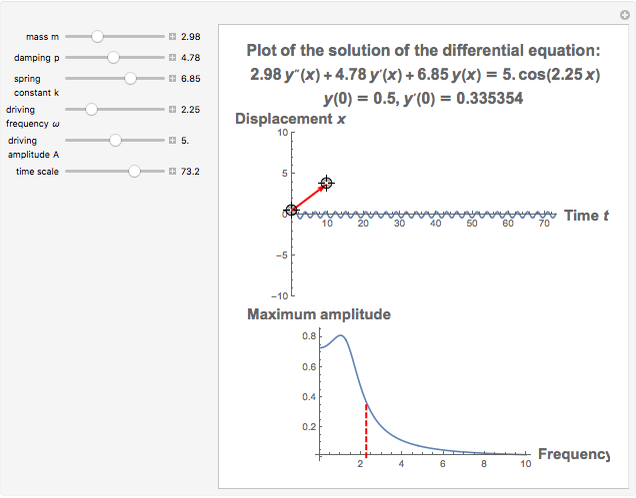
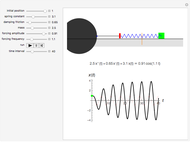
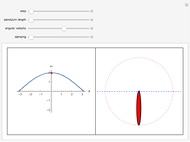
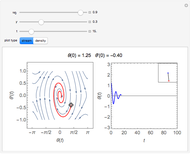
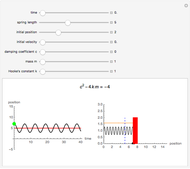
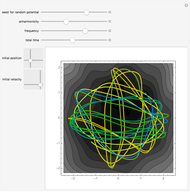
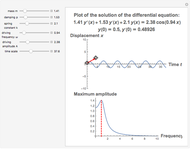
This Demonstration provides a visualization of the classical damped driven harmonic oscillator. The first plot shows the solution of the differential equation; you can choose the initial boundary condition as the tangent to the solution curve at a specified point by dragging the two locators. The second graphic plots the amplitude versus frequency, which peaks at a resonance.

Contributed by: Bartosz Naskrecki (March 2011)
Open content licensed under CC BY-NC-SA

Details

The equation is , where is the mass of a block on a spring, is the damping factor, and is the spring constant. The right-hand side of the equation is the driving force involved in motion. Specifically, it is a periodic force with frequency and amplitude . The boundary condition applied to this equation gives exactly one solution.

The resonance curve of the differential equation is given by , which may have a singularity at the resonance frequency .

Snapshots

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send