Einstein's Most Excellent Proof

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
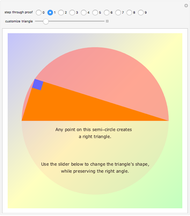
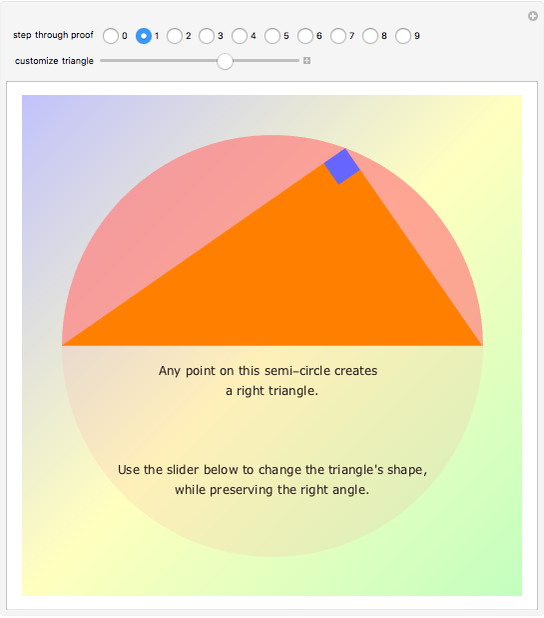
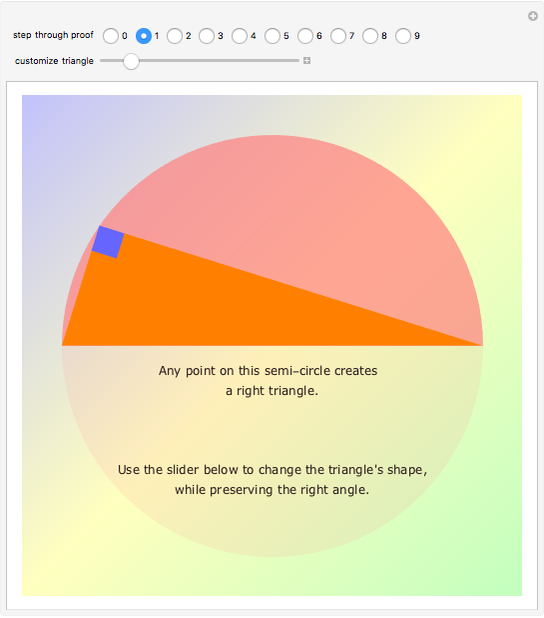
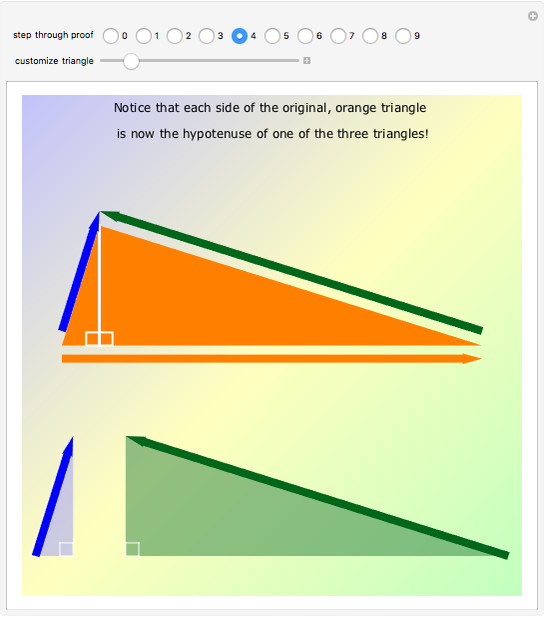
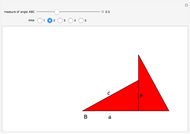
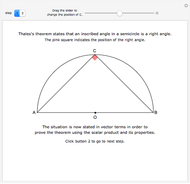
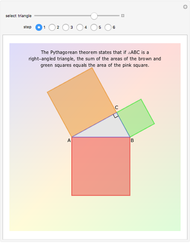
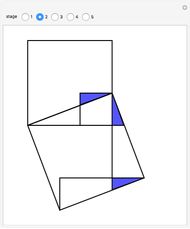
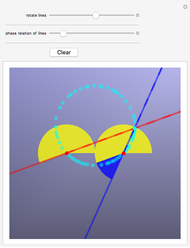
According to his autobiography, a preteen Albert Einstein divised a new proof of the Pythagorean theorem based on the properties of similar triangles. Many known proofs use similarity arguments, but this one is notable for its elegance, simplicity, and the sense that it reveals the connection between length and area that is at the heart of the theorem.
Contributed by: John Kiehl (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Einstein in his autobiography says, "At the age of 12, I experienced a second wonder of a totally different nature: in a little book dealing with Euclidean plane geometry, which came into my hands at the beginning of a school year. Here were assertions, as for example the intersection of the three altitudes of a triangle in one point, which — though by no means evident — could nevertheless be proved with such certainty that any doubt appeared to be out of the question. This lucidity and certainty made an indescribable impression upon me. For example I remember that an uncle told me the Pythagorean theorem before the holy geometry booklet had come into my hands. After much effort I succeeded in "proving'' this theorem on the basis of the similarity of triangles … for anyone who experiences [these feelings] for the first time, it is marvellous enough that man is capable at all to reach such a degree of certainty and purity in pure thinking as the Greeks showed us for the first time to be possible in geometry."
Permanent Citation
"Einstein's Most Excellent Proof"
http://demonstrations.wolfram.com/EinsteinsMostExcellentProof/
Wolfram Demonstrations Project
Published: March 7 2011