Encrypted Secret Sharing

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
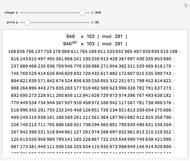
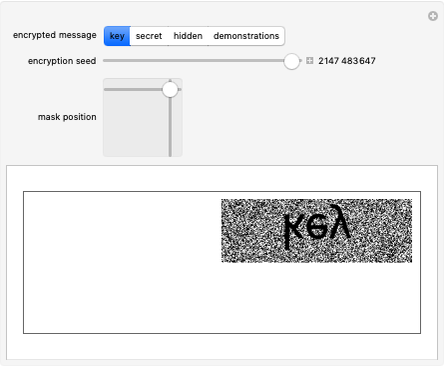
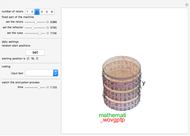
This Demonstration illustrates Adi Shamir’s variable threshold method of sharing a secret among  people, where each person knows their key, and some subset
people, where each person knows their key, and some subset  of those keys is required to recover the secret. The method is based on the fact that a polynomial of degree
of those keys is required to recover the secret. The method is based on the fact that a polynomial of degree  can be reconstructed, given the coordinates of
can be reconstructed, given the coordinates of  points. The reconstruction yields the constant term of the polynomial, which is then the recovered secret. Typical secrets could include various encryption keys, such as the 128–256-bit keys used in the Advanced Encryption Standard (AES).
points. The reconstruction yields the constant term of the polynomial, which is then the recovered secret. Typical secrets could include various encryption keys, such as the 128–256-bit keys used in the Advanced Encryption Standard (AES).
Contributed by: Jim Wiggins (November 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
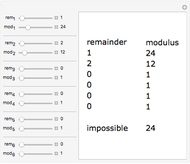
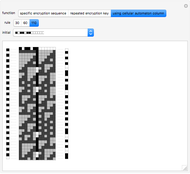
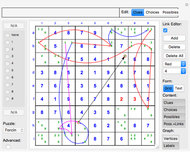
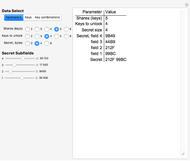
Snapshot 1: five shares are selected, and any combination of four keys is sufficient to recover the secret
Snapshot 2: the "Keys" button in the "Data Select" section is clicked
Snapshot 3: The "Key combinations" button is clicked. The display area shows, in this case, that no combination of two or three keys can recover the secret, but that any combination of four keys does.
References
[1] Wikipedia. "Shamir's Secret Sharing." (Nov 12, 2013) en.wikipedia.org/wiki/Shamir%27 s_Secret _Sharing.
[2] Wikipedia. "Secret Sharing." (Nov 12, 2013) en.wikipedia.org/wiki/Secret_sharing.
[3] Wikipedia. "Finite Field." (Nov 12, 2013) en.wikipedia.org/wiki/Finite_field.
[4] Wikipedia. "Lagrange Polynomial." (Nov 12, 2013) en.wikipedia.org/wiki/Lagrange_polynomial.
[5] Wikipedia. "Advanced Encryption Standard." (Nov 12, 2013) en.wikipedia.org/wiki/Advanced_Encryption_Standard.
Permanent Citation