Wolfram Demonstrations Project

This Demonstration generates all Pythagorean triples (PTs) using a Cantor diagonal ordering to produce all multiples of all primitive PTs. These are, in turn, generated by the Calkin–Wilf (C-W) enumeration of the rational numbers. The

slider sets the number of PTs shown.

Various modes allow graphical or tabular displays of the results, including the "derivation" to show the steps from the positive integers

to the Cantor pair

, to a filtered list of compliant natural numbers, to C-W pairs

, to the PTs of the form

In mode "graph

", a blue point

represents a primitive PT and a red point represents a non-primitive PT; mouse over to see all side lengths and a proportional triangle.

Use the "zoom" slider to zoom into the graph near the origin.

The "Cantor ordering" mode shows how each integer generates a multiplier and a primitive PT; mouse over to see with details. Hover over a point in the graph to see the values

and a proportional triangle.

Contributed by: Colton H. Davis and Kenneth E. Caviness

Slider Zoom
Gamepad Controls
Automatic Animation

This enumeration of all Pythagorean triples (PTs) generates exactly one PT from every natural number, thus creating a comprehensive ordered list of PTs, indexed by the natural numbers. This is done by first creating a two-dimensional table of ordered pairs of the form

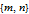
, to be traversed in diagonal stripes (inspired by Cantor's demonstration of the countability of the rational numbers). The integers

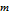
and

are then used as the multiplier and the index of the primitive PT (PPT), for which the precise algorithm is explained more fully in a previous Demonstration. Thus, the function

produces only those C-W pairs of the form

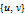
that comply with the conditions that

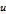
and

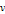
be relatively prime, have opposite parity and

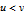
. These pairs are then used to generate PPTs of the form

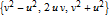
. Multiplying these PPTs by

thus gives a one-to-one mapping between the set of all natural numbers and the set of all PTs.

The "

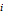
" slider controls how many PTs are calculated, and in graph mode the "zoom" slider determines how much to zoom in on those points close to the origin. Use the "mode" toggle bar to change the display: graphing PTs, generating a simple list of PTs, displaying the Cantor diagonal ordering of

and the

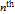
PPT, or generating a commented table showing the derivation of the PTs.

Snapshot 1: the scatter plot graph of the enumerated PTs as given in the

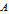
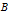
plane, where

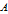
is the odd leg and

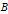
the even leg of the triangle represented by the PT, zoomed in to show only

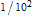
of the largest value, with all side lengths and a proportional triangle shown on mouseover

Snapshot 2: a simple list of the first 50 PTs generated by the enumeration

Snapshot 3: a Cantor diagonal ordering of the first 50 PTs, showing multiplier

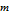
and the PPT indexed by

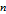
, with values and resultant PTs shown on mouseover

Overlaying diagonal stripes on a doubly infinite table was a clever idea proposed by Georg Cantor to demonstrate the countability of the set of all rationals, which inspired a whole class of countability proofs. The image shown on tab 3 is a modification of one in [1], in which various enumerations are considered. One significant difference between Cantor's scheme, where the enumeration includes an infinite number of duplicate entries, and the present enumeration of all PTs is that here all

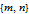
pairs generate distinct PTs, so the algorithm defines a 1-1 and onto function.

Snapshot 4: a table showing all steps of the process: natural numbers,

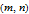
pairs, compliant natural numbers, compliant C-W pairs, PPTs with multipliers and finally PTs generated by the enumeration algorithm

Reference

[1] K. E. Caviness, "Indexing Strings and Rulesets: An Exploration Leading to an Enumeration," The Mathematica Journal, 13, 2011. www.mathematica-journal.com/2011/05/11/indexing-strings-and-rulesets.