Enumerating Pythagorean Triangles

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
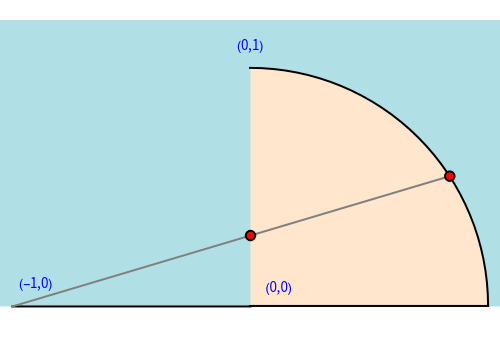
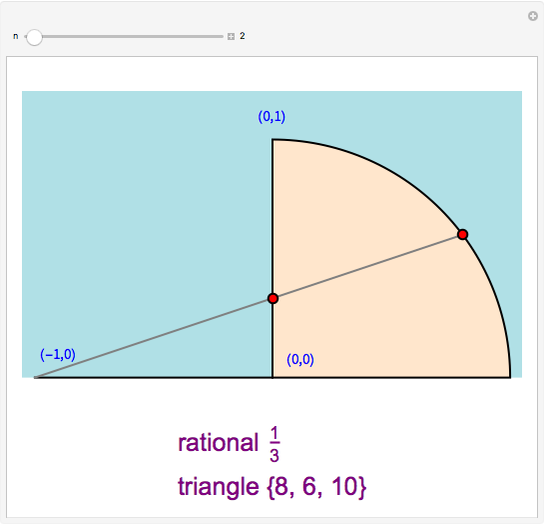
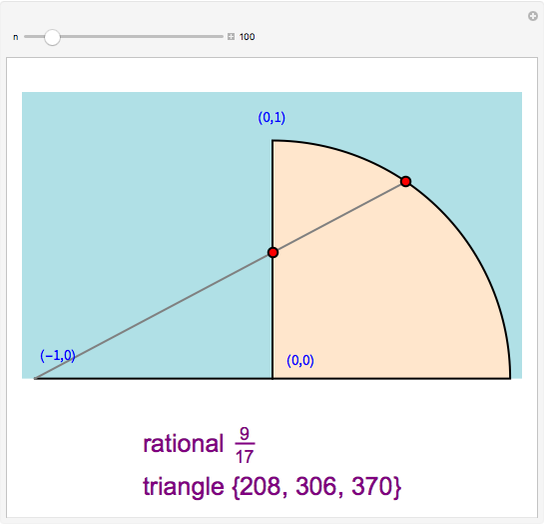
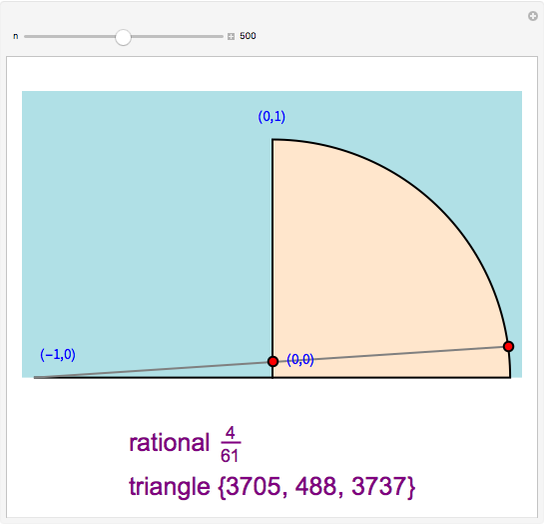
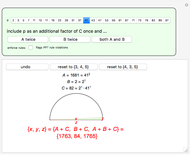
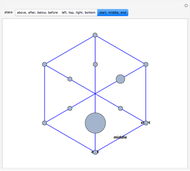
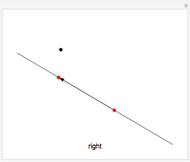
There is a one-to-one correspondence between positive rational numbers  less than 1 and points with positive rational coordinates
less than 1 and points with positive rational coordinates 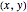 on the unit circle. This correspondence is achieved by joining the point
on the unit circle. This correspondence is achieved by joining the point 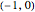 with
with 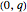 and extending the line to intersect the unit circle at
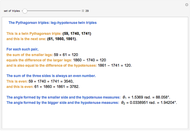
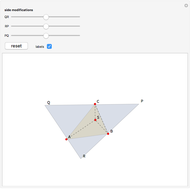
and extending the line to intersect the unit circle at 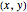 as shown in this Demonstration. As any integral solution of the equation
as shown in this Demonstration. As any integral solution of the equation 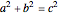 corresponding to a Pythagorean triangle can be put in the form
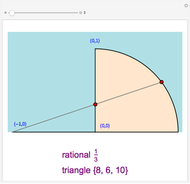
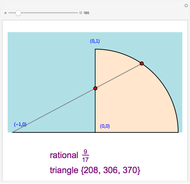
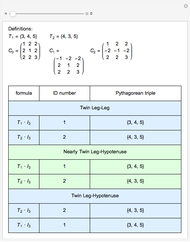
corresponding to a Pythagorean triangle can be put in the form 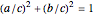 , we can associate Pythagorean triangles with points with positive rational coordinates on the unit circle. This Demonstration shows the
, we can associate Pythagorean triangles with points with positive rational coordinates on the unit circle. This Demonstration shows the 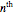 rational number and its associated
rational number and its associated 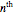 Pythagorean triangle. By varying
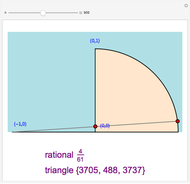
Pythagorean triangle. By varying  , can you find the only Pythagorean triangle with a side equal to 2009 that exists in the given range? Alas, the first rational with a part equal to 2009 is 30/2009 and it occurs at
, can you find the only Pythagorean triangle with a side equal to 2009 that exists in the given range? Alas, the first rational with a part equal to 2009 is 30/2009 and it occurs at 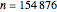 , too far out of our range
, too far out of our range 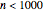 .
.
Contributed by: Jaime Rangel-Mondragon (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Enumerating Pythagorean Triangles"
http://demonstrations.wolfram.com/EnumeratingPythagoreanTriangles/
Wolfram Demonstrations Project
Published: March 7 2011