Finite Limit at a Finite Point
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
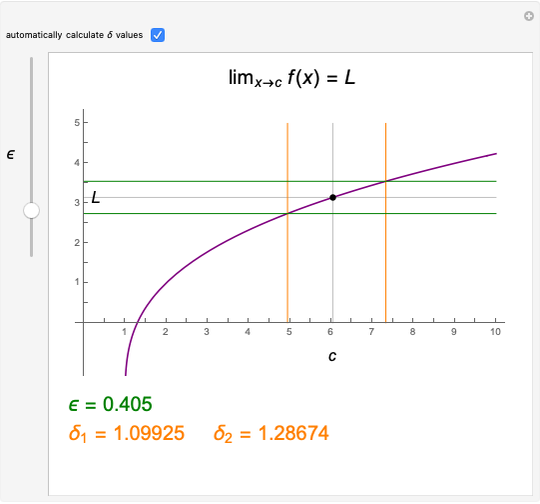
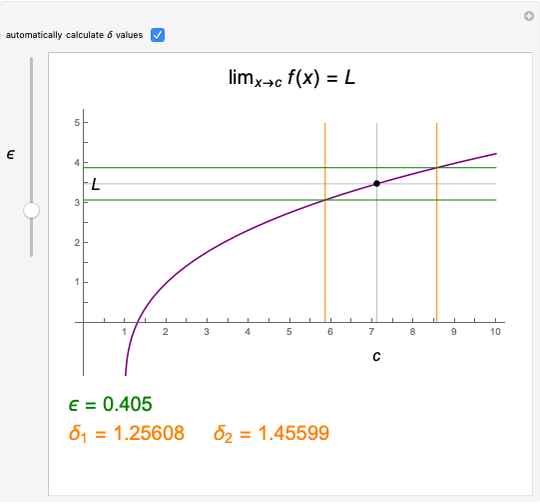
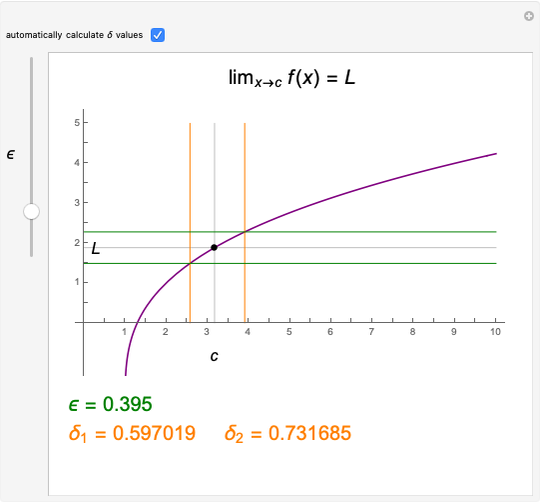
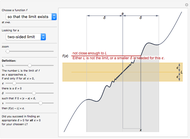
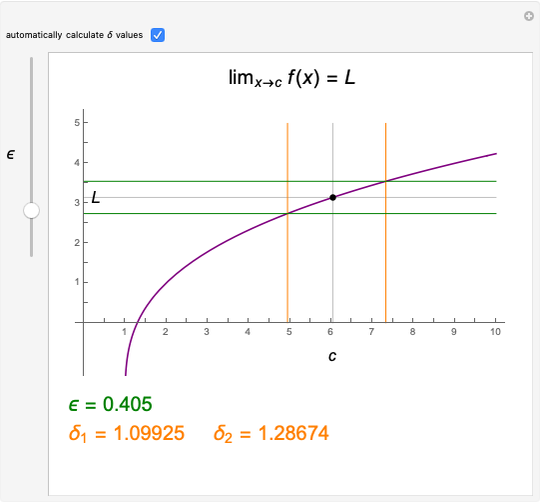
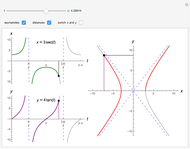
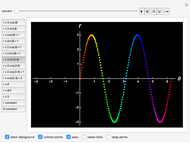
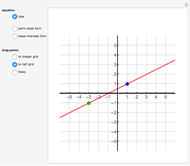
The function 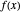 has a finite limit,
has a finite limit, 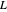 , as
, as 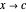 . This means that for any
. This means that for any 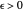 , there is an interval
, there is an interval 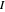 of width
of width 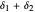 around
around  (perhaps with
(perhaps with 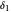 and
and 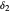 very small), such that
very small), such that 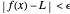 whenever
whenever 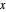 is in the interval
is in the interval 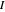 . Move the point directly and vary
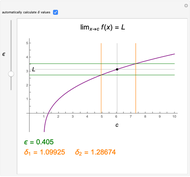
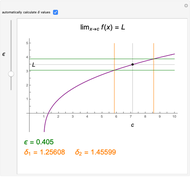
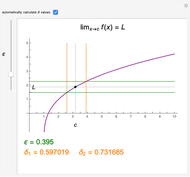
. Move the point directly and vary  using the slider. This Demonstration computes the largest
using the slider. This Demonstration computes the largest 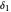 and
and 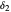 for a given
for a given  so that
so that 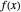 lies between
lies between 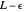 and
and 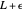 . The values for
. The values for 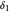 and
and 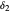 may be found automatically or manually by dragging. The function shown is
may be found automatically or manually by dragging. The function shown is 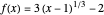 .
.
Contributed by: Abby Brown (March 2011)
Open content licensed under CC BY-NC-SA
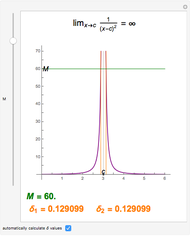
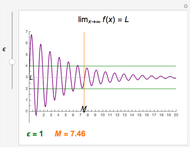
Snapshots
Details
Permanent Citation