Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Geometric Series Based on Area Ratios of Similar Polygons

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

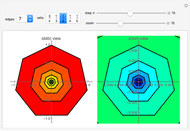
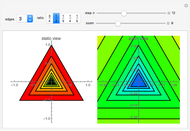
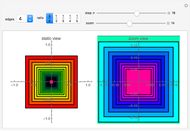
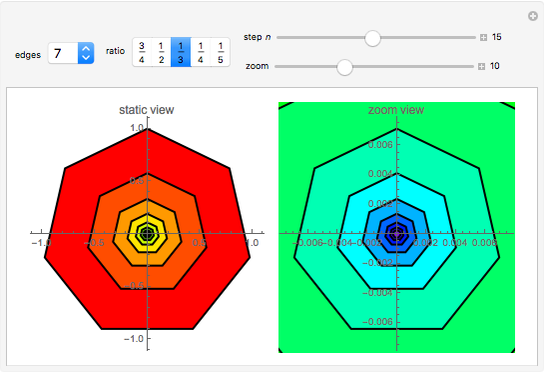
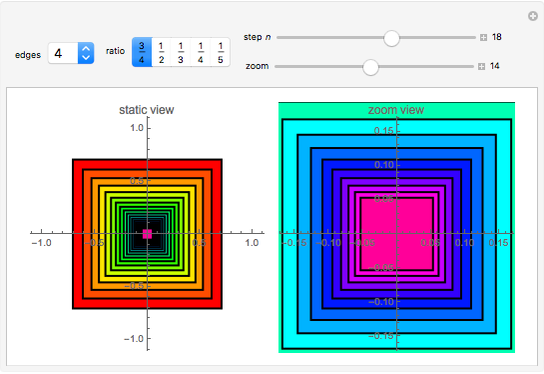
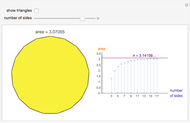
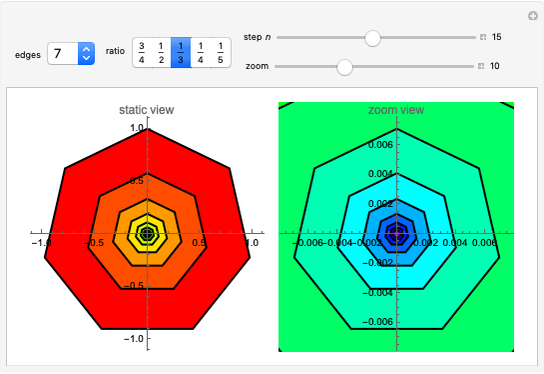
This Demonstration shows a graphical representation of the sum of a convergent geometric series for the area of similar polygons. Let be the area of the original polygon and let be the ratio of one polygon in a sequence to the next.

[more]

Starting from the algebraic identity , as , .

You can choose from five ratios that lie in the interval , and regular polygons that range from 3 to 9 edges, with 15 edges added for fun. Use the "step" slider for the next step of each similar polygon. Use the "zoom" slider to show subsequent terms of the series in greater detail.

[less]

Contributed by: Joshua E. Emrick and Steven M. Hetzler (December 2019)
Open content licensed under CC BY-NC-SA

Details

Let represent the area of the largest polygon. Then , , , … are the areas of the successive smaller polygons. Each polygon's area is equal to the area of a collar: plus the area of a smaller similar polygon . For example, in Snapshot 1, the area of the largest triangle is ; then the area of the next largest triangle is and the area of the collar is .

References

[1] E. M. Markham, "Geometric Series IV," Proofs without Words: Exercises in Visual Thinking (R. B. Nelsen, ed.), Mathematical Association of America, 1993 p. 123.

[2] E. M. Markham, "Proof without Words: Geometric Series," Mathematics Magazine, 66(4), 1993 p. 242. doi:10.2307/2690738.

Snapshots

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send