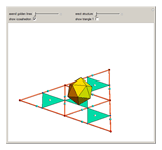
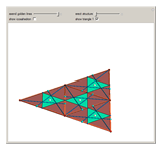
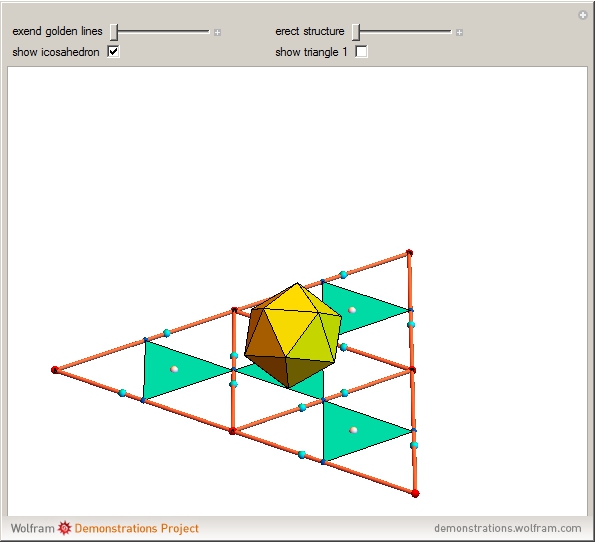
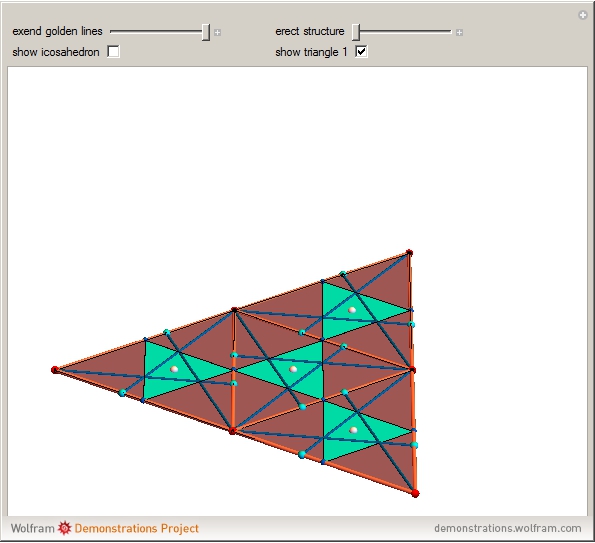
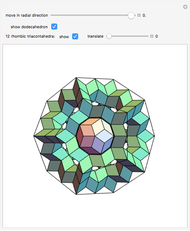
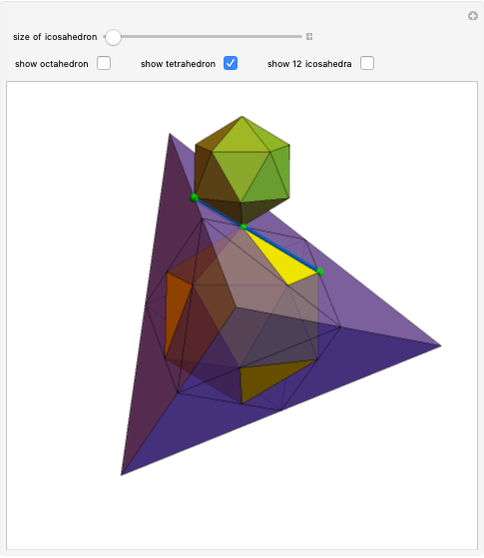
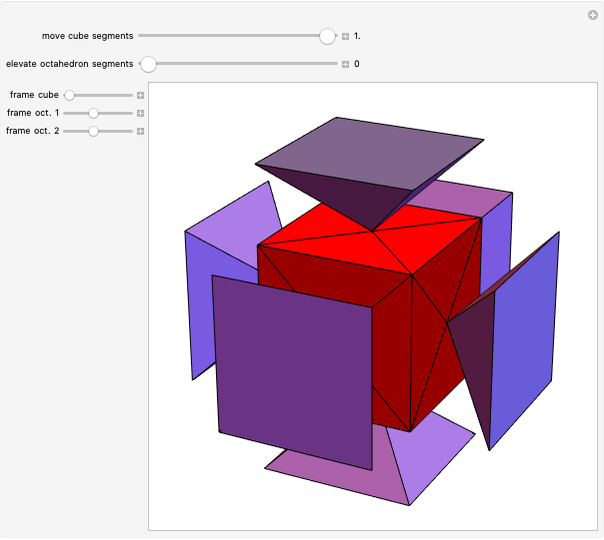
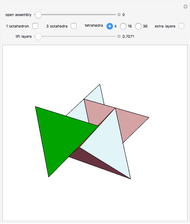
Define a golden line in an equilateral triangle as the line that connects a vertex of the triangle to the point on the opposite edge that divides the edge in the golden ratio 1:. Each of the three golden lines is divided by its intersections into three parts of sizes 1, , and . The points of intersection coincide with the vertices of the regular icosahedron, octahedron, and tetrahedron. Dragging the "erect structure" slider folds the four triangles into a tetrahedron.