Golden Truncated Icosahedron

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
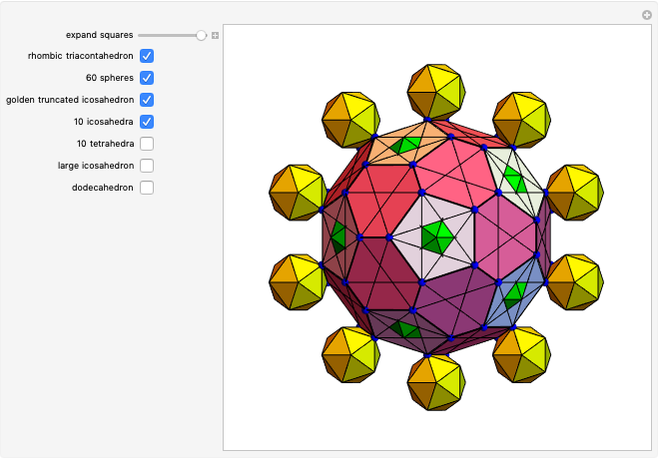
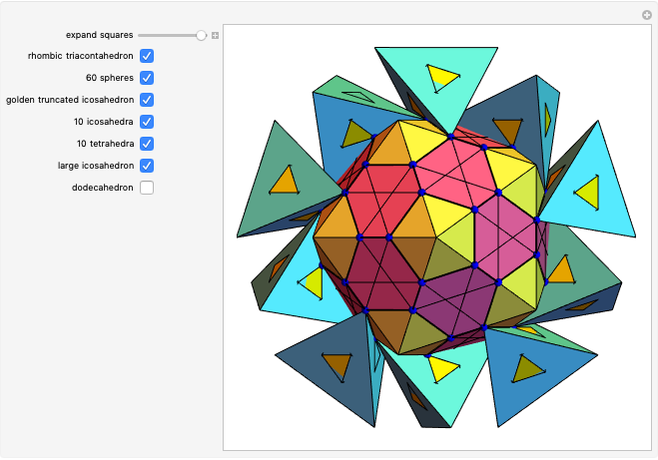
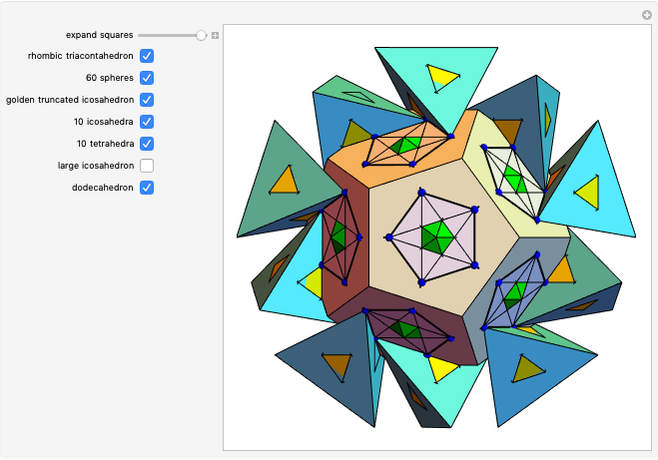
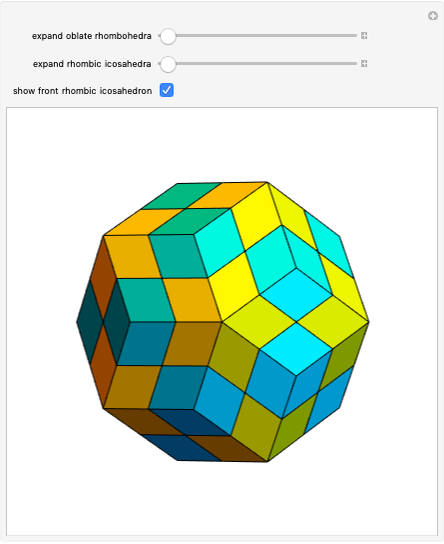
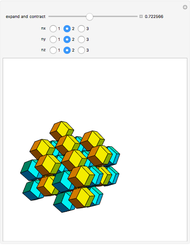
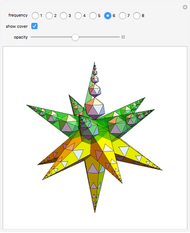
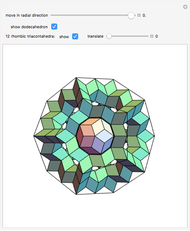
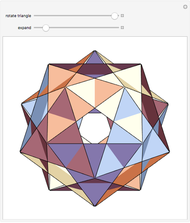
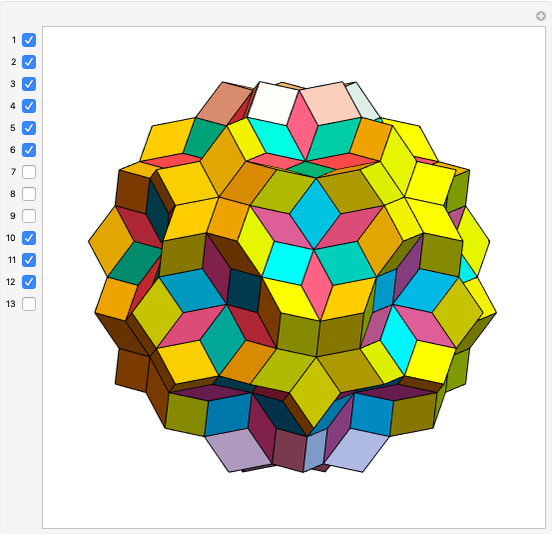
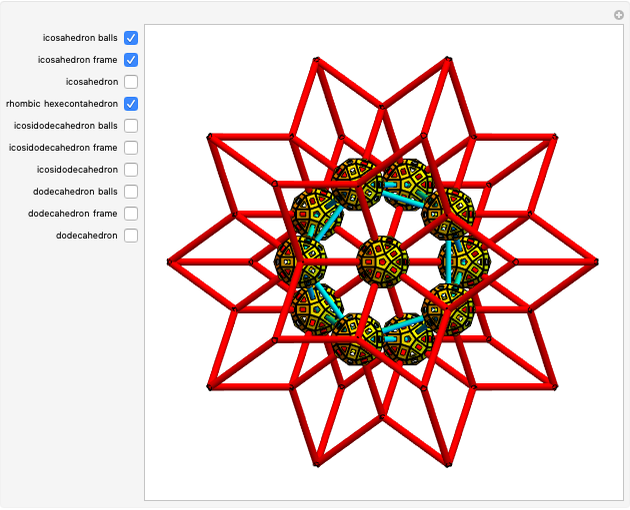
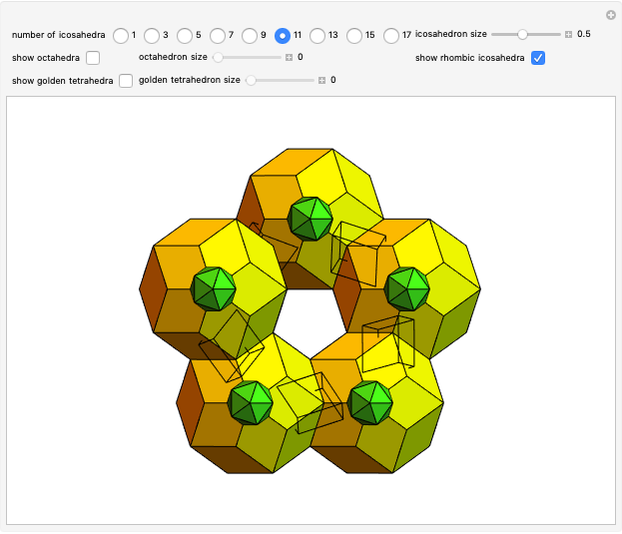
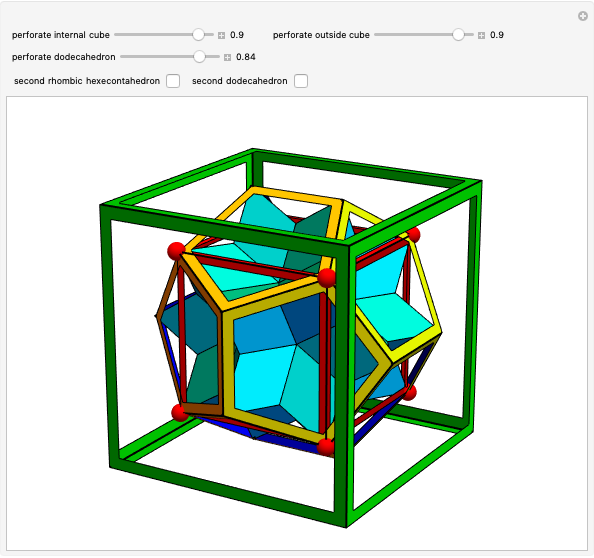
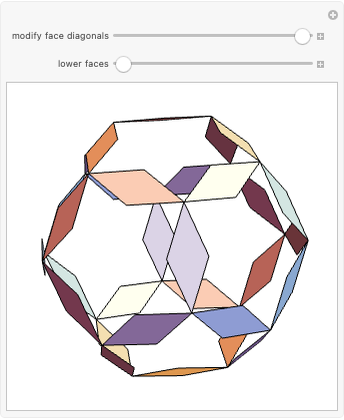
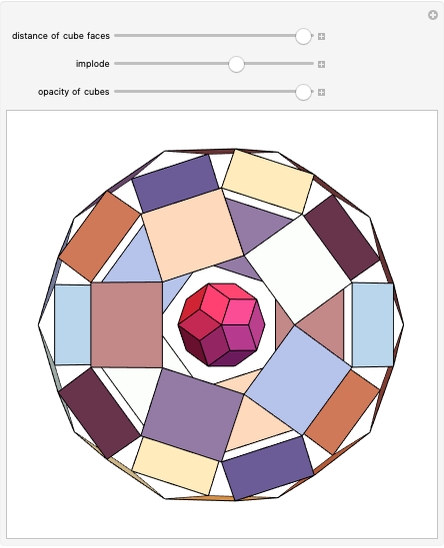
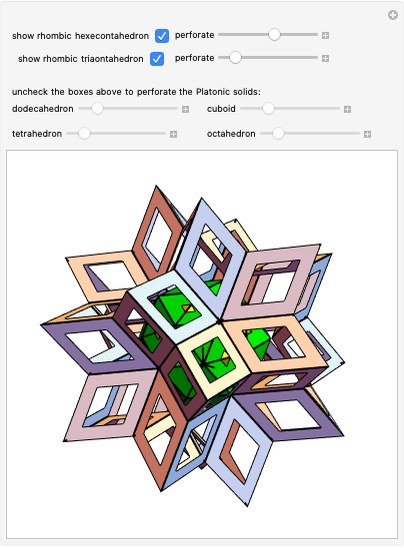
A truncated icosahedron with golden hexagonal faces is defined here as a golden truncated icosahedron (GTICO). When 30 squares fitted with vertex connections on a rhombic triacontahedron (RT) are expanded by the golden ratio, then the vertices meet again. These meeting points correspond to the vertices of a GTICO. In this Demonstration, the GTICO is related to a number of shapes. The most notable features include: (1) in a ring of 10 tetrahedra, the vertices of the tetrahedra are on the vertices of the GTICO; (2) the edges of the rings of 10 icosahedra coincide with the shorter edge of the golden hexagons; (3) icosahedra in the ring meet the tips of pentagrams; and (4) the edges of expanded squares divide the faces of the GTICO and the large icosahedron in various proportions related to the golden ratio.
Contributed by: Sándor Kabai (August 2022)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Some observations:
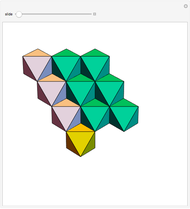
• The 30 squares correspond to the square faces of a small rhombicosidodecahedron (SRD).
• A compound of five cubes could be obtained if the expansion was continued beyond the meeting points.
• The lower edges of the tetrahedra lie across the initial squares (faces of RT and SRD).
• The edges of expanded squares trace out pentagrams, which could be best seen on the faces of the dodecahedron and GTICO.
• The tips of RT fit into the central pentagons of the pentagrams.
• The 10 tetrahedra are part of that cluster of 30 (not shown). The occurrences of the golden ratio are abundant (it could be an exciting challenge to count them).
Permanent Citation