Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Horizontal Visibility Graphs for Elementary Cellular Automata

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

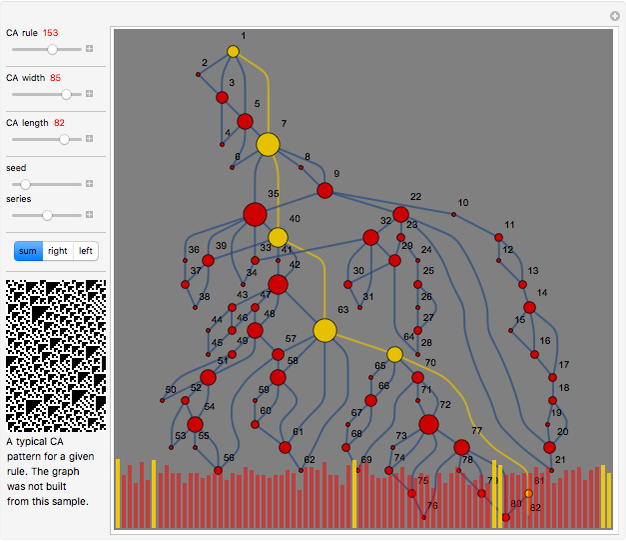
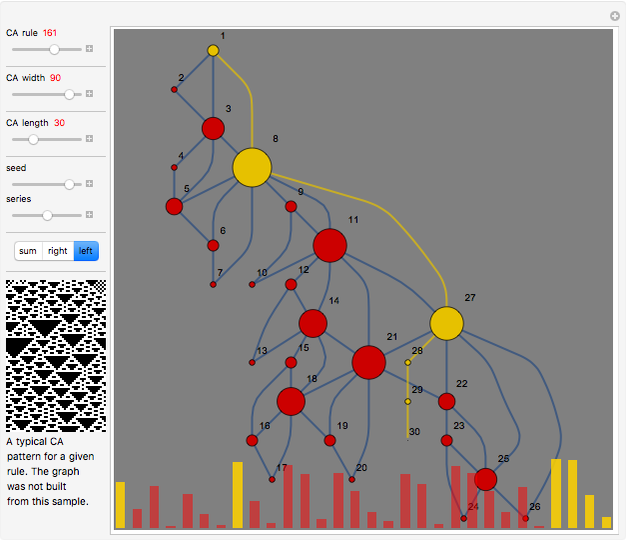
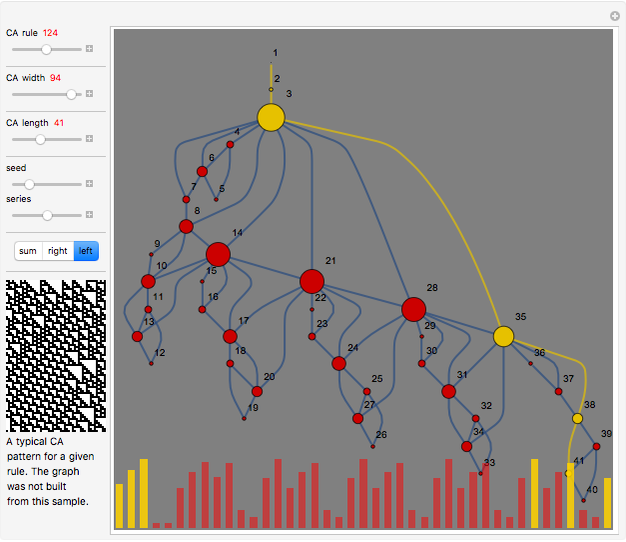
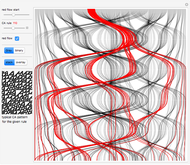
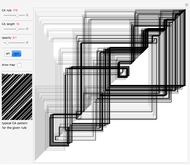
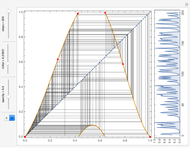
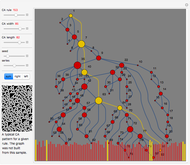
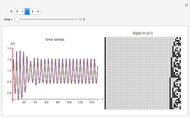
A time series can be formed from an evolution of a finite elementary cellular automaton (ECA). This can be done in a few different ways. We can consider every step of an ECA evolution to be a binary number and calculate its decimal form by counting digits from left to right or in reverse. We also could just sum the digits. These operations are reflected correspondingly in the control buttons "left," "right," and "sum."

[more]

The Demonstration constructs the horizontal visibility graph (HGV) for an ECA time series. An HVG maps a time series to a graph. Each event in the time series corresponds to a vertex in the graph. Two vertices are connected by an edge if the corresponding events in the time series are larger than all the events between them.

The goal of mapping time series to graphs is to apply powerful graph-theoretic methods to time series analysis. To illustrate this, let us consider a toy problem. Vertical posts of various heights are arranged along a straight line, and each can emit a horizontal signal from any point along its height. If a signal needs to be communicated from the first to the last post, what is the minimum set of posts necessary? While the posts are considered as a time series, the problem is solved as a graph-theoretic shortest-path algorithm. The solution is highlighted in yellow.

[less]

Contributed by: Vitaliy Kaurov (February 2013)
Open content licensed under CC BY-NC-SA

Snapshots

Details

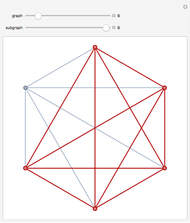
There are various mappings from time series to visibility graphs. HVG is one of the simplest algorithms. Some more elaborate schemes claim a partial inverse operation. The main idea behind these mappings is their ability to apply time series and signal processing tools to graphs and metrics of graphs to time series. This may lead to discoveries of new relationships and a better understanding of old ones.

References

[1] A. S. L. O. Campanharo, M. I. Sirer, R. D. Malmgren, F. M. Ramos, and L. A. N. Amara, "Duality between Time Series and Networks," PLoS One, 6(8), 2011 e23378. www.ncbi.nlm.nih.gov/pmc/articles/PMC3154932.

[2] L. Lacasa, B. Luque, F. Ballesteros, J. Luque, J. C. Nuño, "From Time Series to Complex Networks: The Visibility Graph," PNAS, 105(13), 2008 pp. 4972–4975. www.pnas.org/content/105/13/4972.full.

[3] B. Luque, L. Lacasa1, F. Ballesteros, and J. Luque, "Horizontal Visibility Graphs: Exact Results for Random Time Series," Physical Review E, 80(4), 046103, 2009. pre.aps.org/abstract/PRE/v80/i4/e046103.

[4] V. Fioriti, A. Tofani, and A. Di Pietro, "Discriminating Chaotic Time Series with Visibility Graph Eigenvalues," Complex Systems, 21(3), 2012 pp. 193–200. www.complex-systems.com/abstracts/v21_i03_a03.html.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send