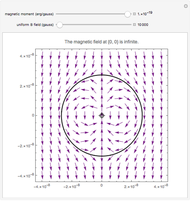
Integrating a Vector Field along a Curve

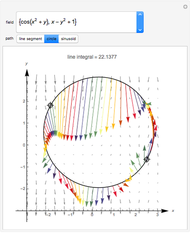
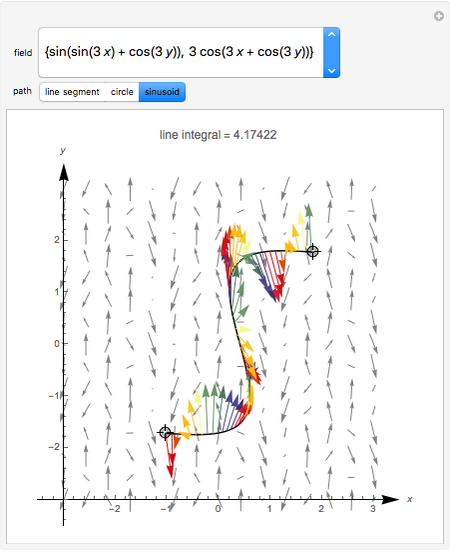
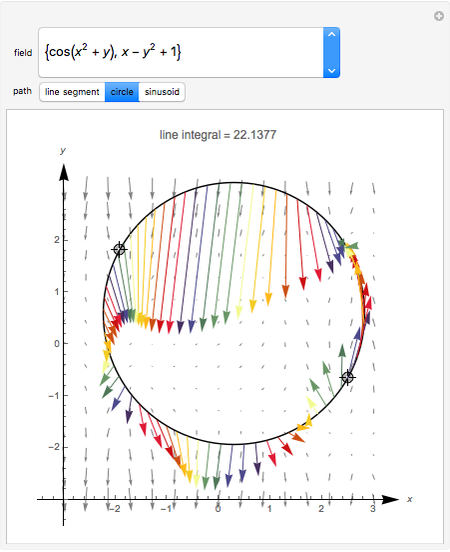
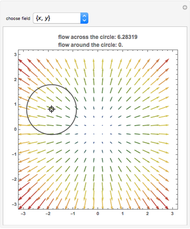
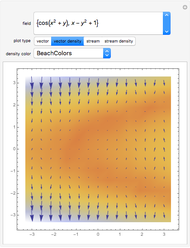
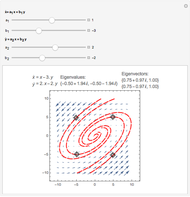
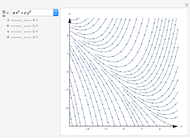
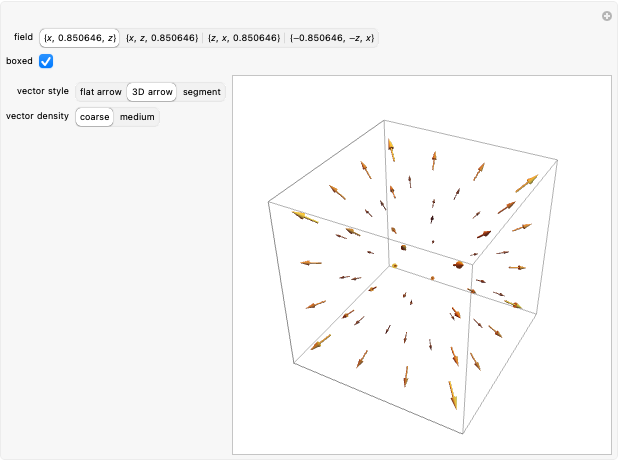
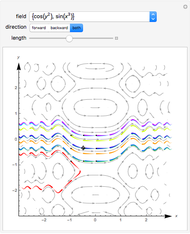
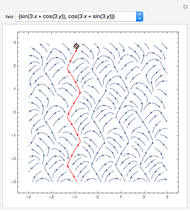
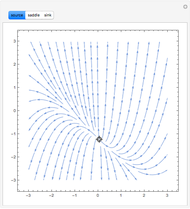
The line integral 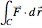of the vector field 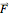along the curve 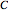gives the work done by the field on an object moving along the curve through the field. A field is called conservative if only the starting and ending points matter; in a conservative field the work done around a closed curve is zero. The first two fields in the popup menu are conservative.