Logarithmic Integral on the Critical Line
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
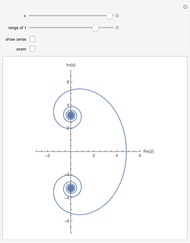
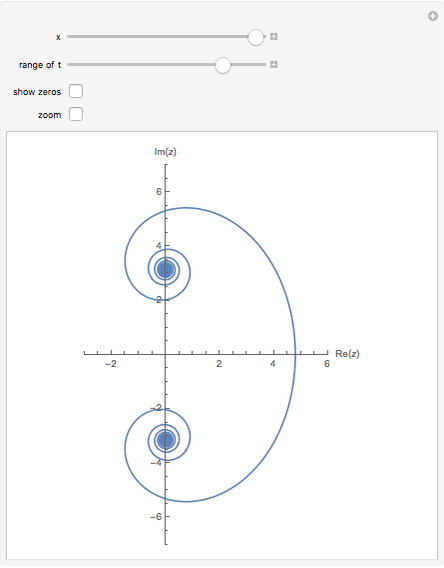
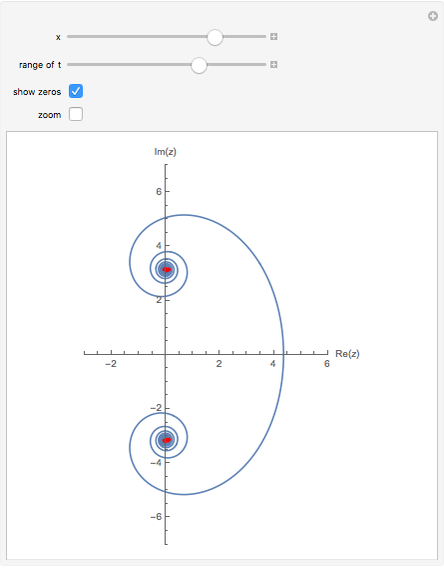
In his 1859 paper "On the Number of Primes Less Than a Given Magnitude," Bernhard Riemann gave a formula involving his zeta function to determine the number of primes less than a specific number 
. This Demonstration shows the behavior of the logarithmic integral 
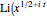) that corresponds to the second or "periodic" terms as referred to by Riemann.
Contributed by: Brandon Carter (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
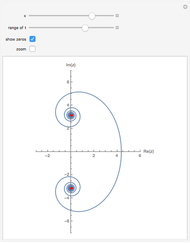
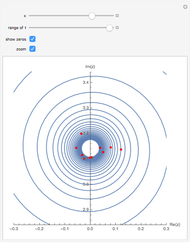
An option is given to show the non-trivial zeros of the zeta function.
Permanent Citation
"Logarithmic Integral on the Critical Line"
http://demonstrations.wolfram.com/LogarithmicIntegralOnTheCriticalLine/
Wolfram Demonstrations Project
Published: March 7 2011
Trigonometric Integral Functions
Rob Morris
Two Integral Mean Value Theorems of Flett Type
Soledad María Sáez Martínez and Félix Martínez de la Rosa
Riemann Sums
Ed Pegg Jr
Riemann versus Lebesgue
Francisco J. Freniche
Riemann Sums: A Simple Illustration
Phil Ramsden
Graphs of the Beta Function
Daniel de Souza Carvalho
Incomplete Gamma Function with Continued Fractions
Andreas Lauschke
Boole Differential Equation with Continued Fractions
Andreas Lauschke
Lebesgue Integration
Anton Antonov
Some Gaussian Integrals
Casimir Kothari
