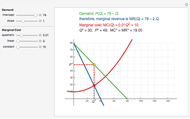
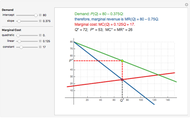
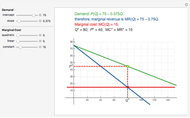
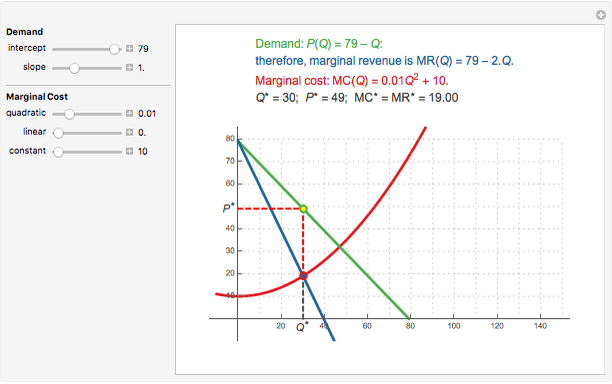
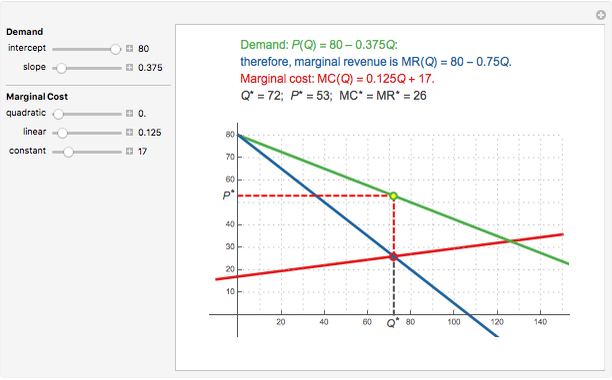
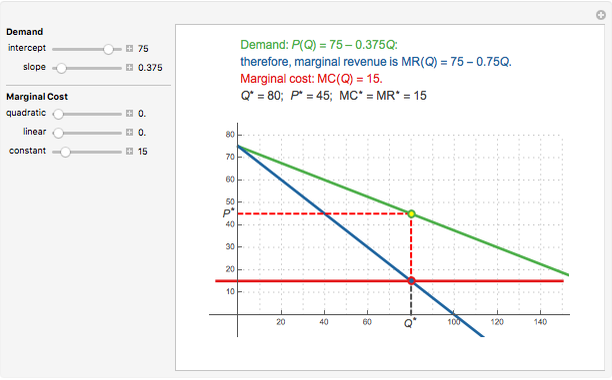
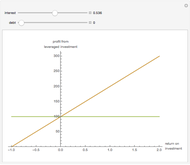
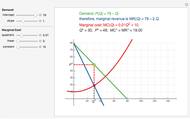
A firm possessing market power faces a downward-sloping demand curve. An important consequence of the firm's market power is that its marginal revenue is less than price. If the firm produces in the short run, the profit-maximizing output is found where marginal cost equals marginal revenue. This Demonstration shows a linear demand curve (green), its associated marginal revenue curve (blue), and the firm's marginal cost curve (red); mouse over the curves to identify them. The point where the marginal revenue and marginal cost curves intersect is identified as well as the point the firm uses to set the profit-maximizing price; mouse over these points to identify them.