Ordinary and Extraordinary Refractive Indices in a 2D Anisotropic Crystal

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
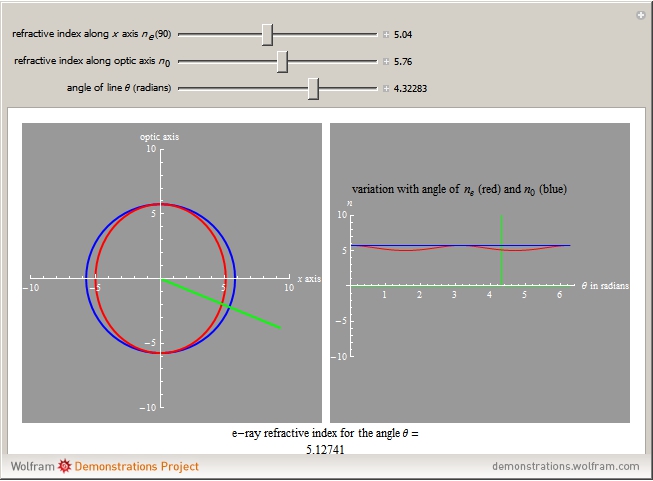
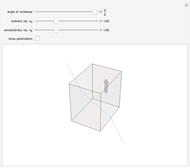
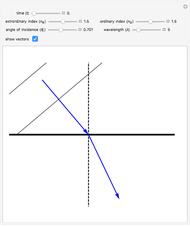
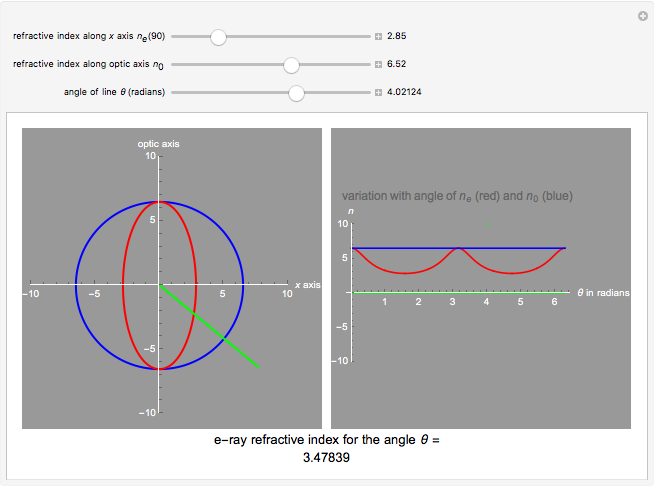
This Demonstration shows how the refractive index of an e-ray and an o-ray change with the angle  with respect to the optic axis in a 2D anisotropic crystal. It shows the shapes of the refractive indices of both negative and positive crystals and the plots show how the values of the refractive indices change in different directions inside a crystal.
with respect to the optic axis in a 2D anisotropic crystal. It shows the shapes of the refractive indices of both negative and positive crystals and the plots show how the values of the refractive indices change in different directions inside a crystal.
Contributed by: Dileep Kottilil (March 2013)
Open content licensed under CC BY-NC-SA
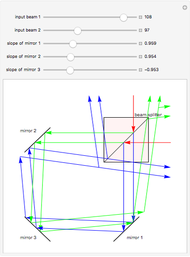
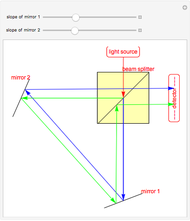
Snapshots
Details
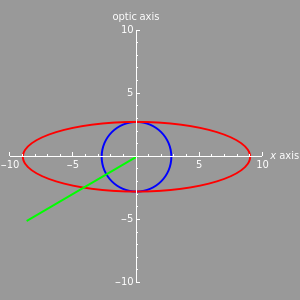
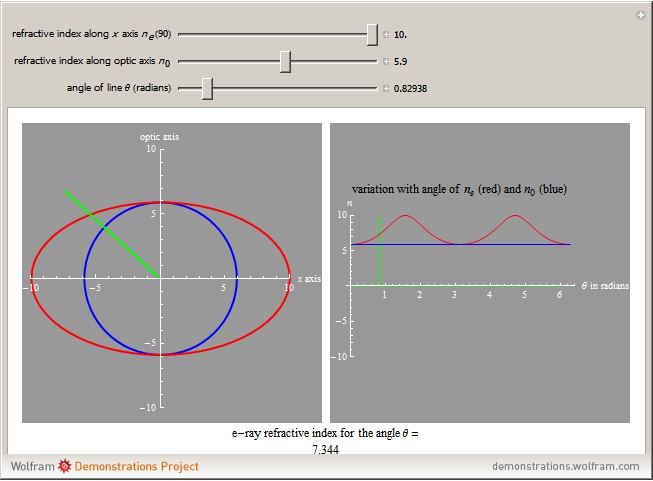
The figure on the left shows the shapes of the refractive indices for both ordinary and extraordinary rays in an anisotropic crystal (o-ray in blue and e-ray in red). The rays have the same refractive index on the vertical optic axis. The green line indicates the direction inside of the crystal along which the refractive indices are considered. By varying  (defined as the angle between the optic axis and the green line), we could change our direction inside the crystal. For different angles, the refractive indices for the two rays are different, which is why we get two different shapes. The o-ray refractive index is the same for all angles, but for the e-ray it has the shape of an ellipse. The difference between the values of the refractive indices of the two rays is the maximum at 90 degrees.
(defined as the angle between the optic axis and the green line), we could change our direction inside the crystal. For different angles, the refractive indices for the two rays are different, which is why we get two different shapes. The o-ray refractive index is the same for all angles, but for the e-ray it has the shape of an ellipse. The difference between the values of the refractive indices of the two rays is the maximum at 90 degrees.
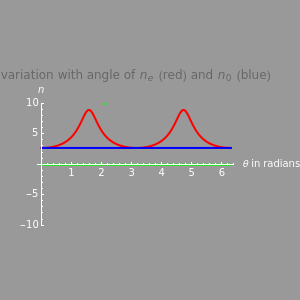
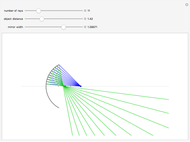
The second figure shows qualitatively how the values of the refractive indices vary for different directions in a crystal (which is described by the angle  ). If we assume that light is emitted from the origin in all directions, then (in the 2D case) the variation of the refractive index with the direction inside the crystal will give different velocities in different directions. The e-ray and o-ray move at different velocities. If we know the values of the refractive indices, we can determine the velocity of the ray in that particular direction.
). If we assume that light is emitted from the origin in all directions, then (in the 2D case) the variation of the refractive index with the direction inside the crystal will give different velocities in different directions. The e-ray and o-ray move at different velocities. If we know the values of the refractive indices, we can determine the velocity of the ray in that particular direction.
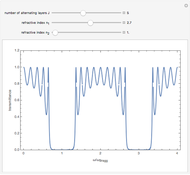
"ne(90)" represents the value of the e-ray refractive index for  and "
and "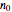 " shows that of the o-ray. Varying
" shows that of the o-ray. Varying  shows the calculated value. The "ne" value for any angle
shows the calculated value. The "ne" value for any angle  is shown below the plots. We also could know the shapes of the refractive index for positive and negative crystals. For positive crystals we should change the values of "ne(90)" and "
is shown below the plots. We also could know the shapes of the refractive index for positive and negative crystals. For positive crystals we should change the values of "ne(90)" and "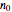 " such that "ne(90)" > "
" such that "ne(90)" > "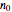 ". If the values are otherwise, we are dealing with negative crystals.
". If the values are otherwise, we are dealing with negative crystals.
This Demonstration also shows the regions inside a anisotropic crystal where the velocities of the rays are the minimum and maximum. From these plots it is obvious that for positive crystals, the minimum velocity of light is at 90 degrees and the maximum is along the optic axis. And for negative crystals, we get the minimum velocity of light along the optic axis and the maximum at 90 degrees, since the velocity is inversely proportional to the refractive index.
Permanent Citation