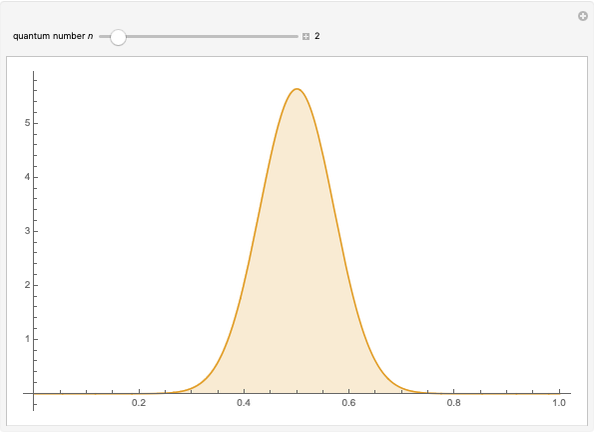
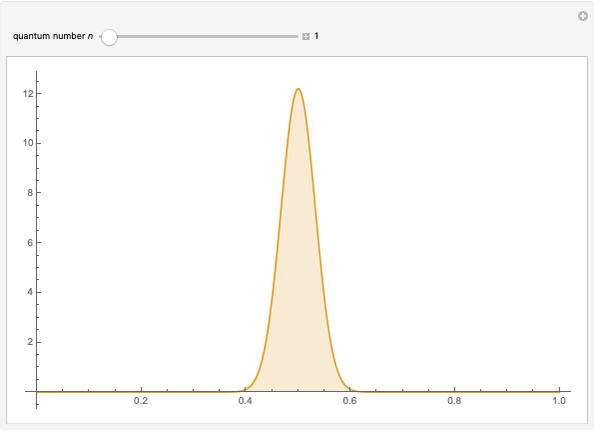
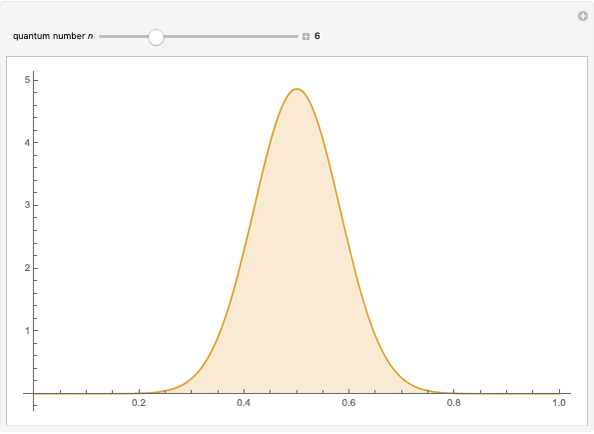
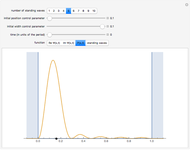
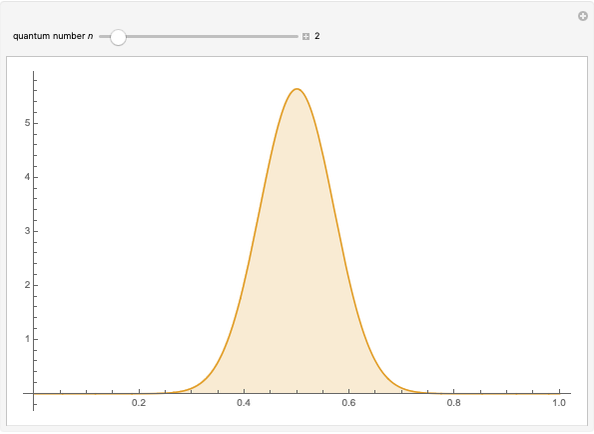
The square of the absolute value of the Schrödinger wavefunction equals the probability density of finding a particle at any point in a box. It is relatively straightforward to show that for all values of , the average or expectation value of the position of the particle will be at the exact midpoint of the box (, where is the length of the box) [1]. The variance, however, increases with increasing quantum number, to a limiting value of . This Demonstration plots the probability density (in blue) and a normal distribution (in yellow) with mean and variance to represent the change in the variance with increasing .