Permutation Sorting
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
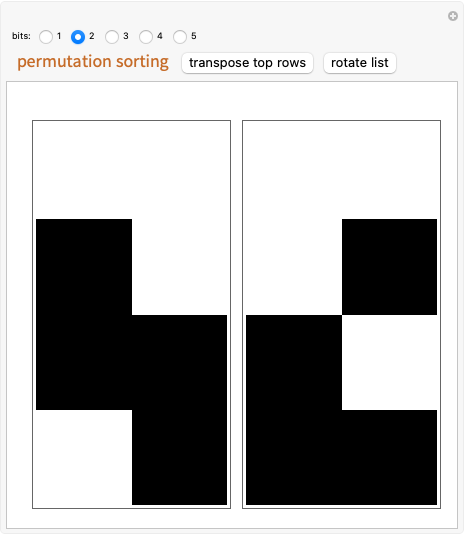
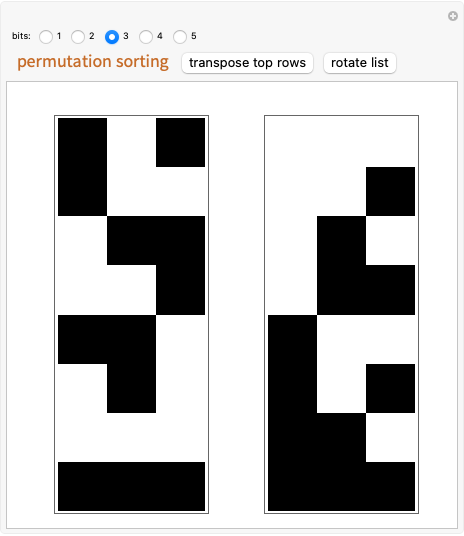
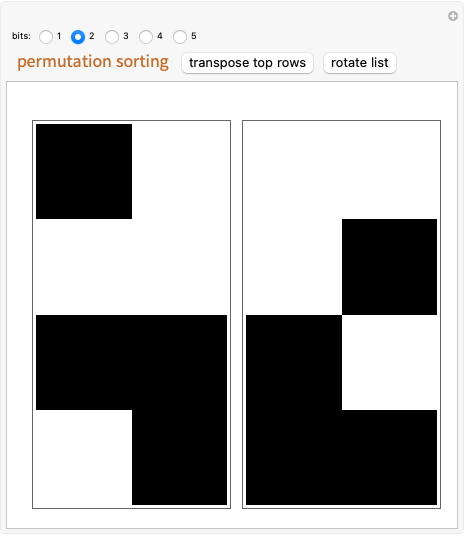
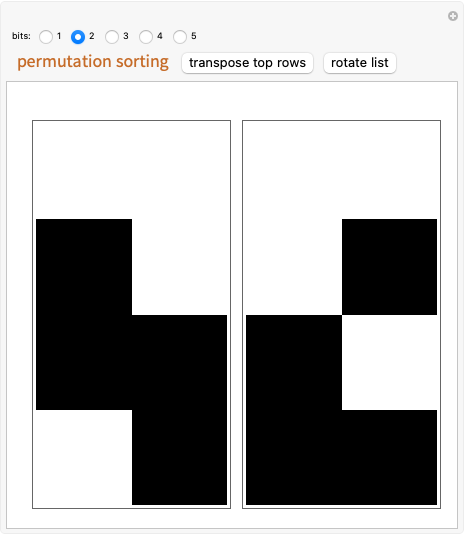
The array plots represent a permutation of a given number of bits. The challenge is to transform the permutation on the right into the randomized permutation on the left using two simple operations: "transpose top rows" and "rotate list." This represents a manual version of a rudimentary algorithm for matching a permutation's binary representation from the original state.
[more]
Contributed by: Benjamin Peter (August 27)
Open content licensed under CC BY-NC-SA
Details
Snapshots
Permanent Citation