Point Spread and Modulation Transfer Functions for Seidel Aberrations

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
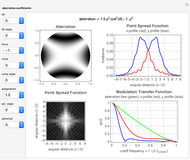
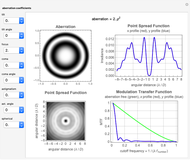
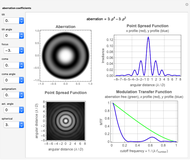
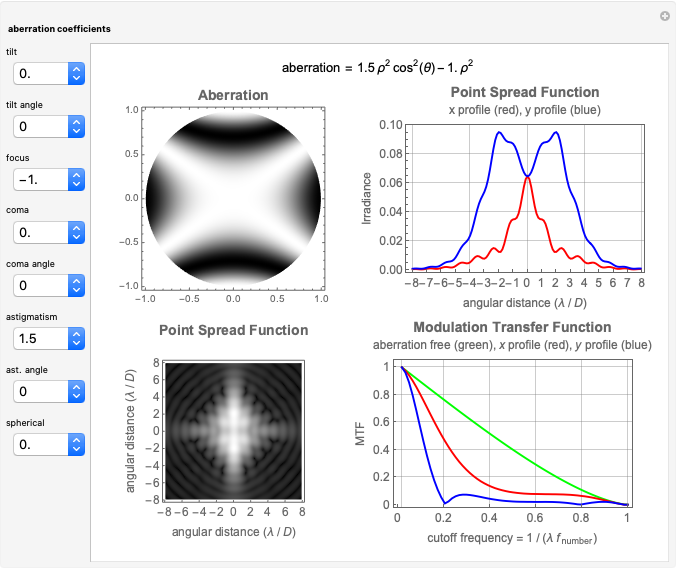
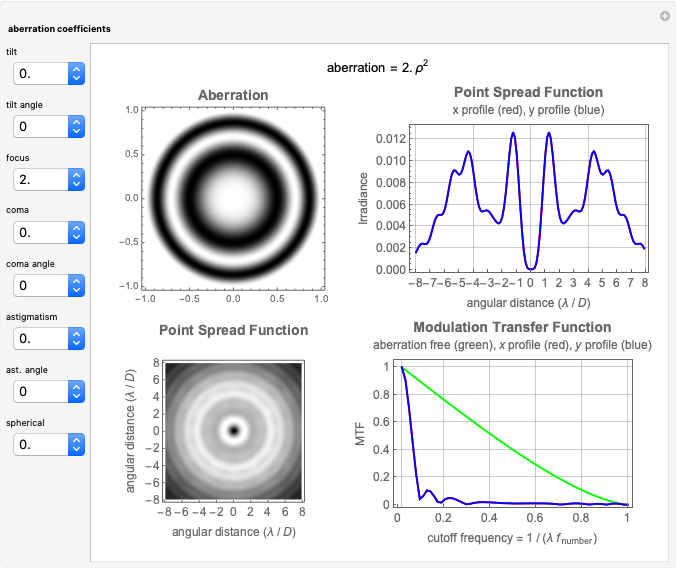
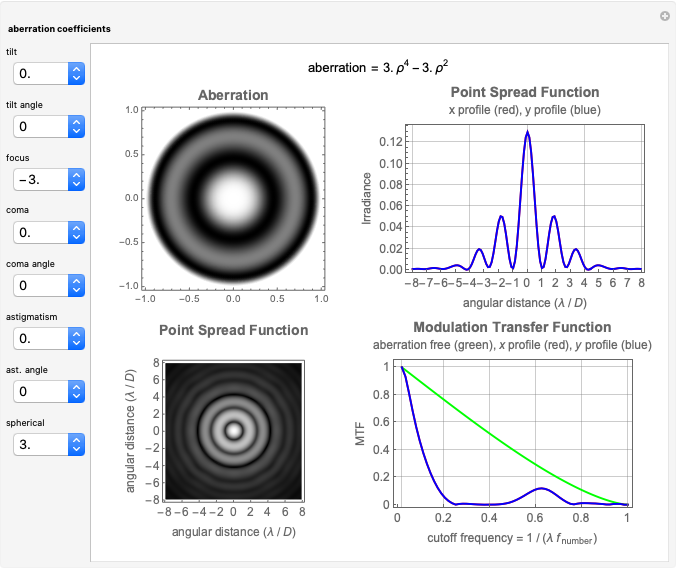
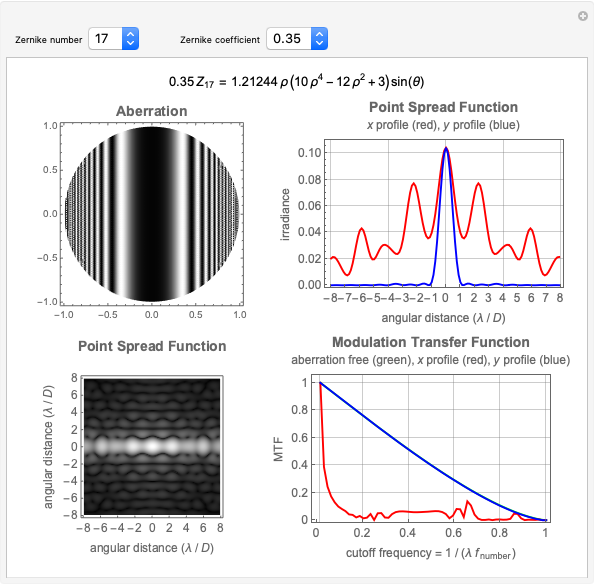
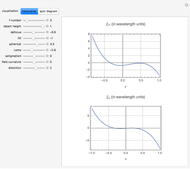
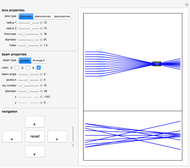
This Demonstration shows the following: an aberration density plot,  and
and  profiles and a density plot of the point spread function, and
profiles and a density plot of the point spread function, and  and
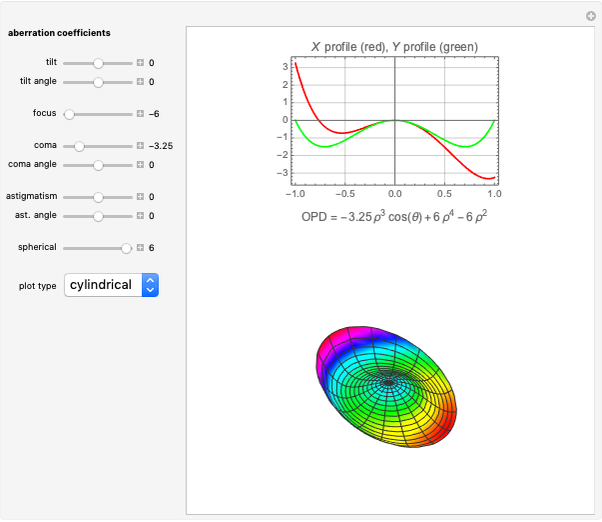
and  profiles of the modulation transfer function. These apply to a wavefront with varying tilt, focus, and fourth-order wavefront aberration coma, astigmatism, and spherical aberration. You can select the coefficients for the different terms making up the aberrated wavefront and vary the angle (orientation) for tilt, coma, and astigmatism.
profiles of the modulation transfer function. These apply to a wavefront with varying tilt, focus, and fourth-order wavefront aberration coma, astigmatism, and spherical aberration. You can select the coefficients for the different terms making up the aberrated wavefront and vary the angle (orientation) for tilt, coma, and astigmatism.
Contributed by: James C. Wyant (February 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This Demonstration details the point spread functions (PSF) and modulation transfer functions (MTF) associated with the Seidel monochromatic aberrations. These were named after L. Seidel, who in 1856 gave explicit formulas for calculating them. The Seidel aberrations are of the fourth degree in the pupil variables  and
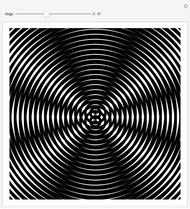
and  and the field position when expressed as wavefront aberrations, and are of the third degree when expressed as transverse ray aberrations. Because of this, these aberrations are either known as third-order or fourth-order aberrations, depending upon whether transverse ray or wavefront aberrations are being considered. The five Seidel aberrations are coma, astigmatism, spherical aberration, distortion, and field curvature. At a given field position, distortion and field curvature are simply tilt and focus (curvature), respectively. The density plot shows what an interferogram would look like testing an optical system with a given amount of tilt, focus, coma, astigmatism, and spherical aberration.
and the field position when expressed as wavefront aberrations, and are of the third degree when expressed as transverse ray aberrations. Because of this, these aberrations are either known as third-order or fourth-order aberrations, depending upon whether transverse ray or wavefront aberrations are being considered. The five Seidel aberrations are coma, astigmatism, spherical aberration, distortion, and field curvature. At a given field position, distortion and field curvature are simply tilt and focus (curvature), respectively. The density plot shows what an interferogram would look like testing an optical system with a given amount of tilt, focus, coma, astigmatism, and spherical aberration.
The PSF, which is given by the square of the absolute value of the Fourier transform of the wavefront, shows what the intensity image of a point source would look like. The  axis of the PSF plot shows angular distance in units of the wavelength,
axis of the PSF plot shows angular distance in units of the wavelength,  , divided by the optical system's pupil diameter,
, divided by the optical system's pupil diameter,  .
.
The MTF, which is given by the magnitude of the Fourier transform of the point spread transfer function, gives the spatial frequency transfer function of an incoherent optical system. The cutoff frequency is given by  , where
, where  is the wavelength, and
is the wavelength, and  is the
is the  -number (or focal ratio) of the optical system given by the focal length divided by the pupil diameter.
-number (or focal ratio) of the optical system given by the focal length divided by the pupil diameter.
References
[1] C-J. Kim and R. R. Shannon, "Catalog of Zernike Polynomials," in Applied Optics and Optical Engineering, Vol. X (R. R. Shannon and J. C. Wyant, eds.), San Diego: Academic Press, 1987 pp. 193–221.
[2] J. W. Goodman, Introduction to Fourier Optics, 3rd ed., Greenwood Village, CO: Roberts & Company, 2004.
[3] V. N. Mahajan, "Zernike Polynomial and Wavefront Fitting," in Optical Shop Testing (D. Malacara, ed.), 3rd ed., Hoboken, NJ: Wiley, 2007 pp. 498–546.
[4] V. N. Mahajan, Optical Imaging and Aberrations, Part II: Wave Diffraction Optics, Bellingham, WA: SPIE Press, 2001.
[5] J. C. Wyant and K. Creath, "Basic Wavefront Aberration Theory for Optical Metrology," in Applied Optics and Optical Engineering, Vol. XI (R. R. Shannon and J. C. Wyant, eds.), New York: Academic Press, 1992 pp. 11–53.
[6] J. C. Wyant. "webMathematica and LiveGraphics3D." (Feb 12, 2013) wyant.optics.arizona.edu/math.htm.
Permanent Citation