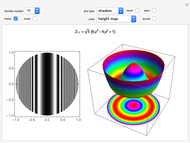
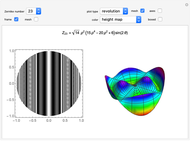
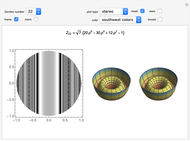
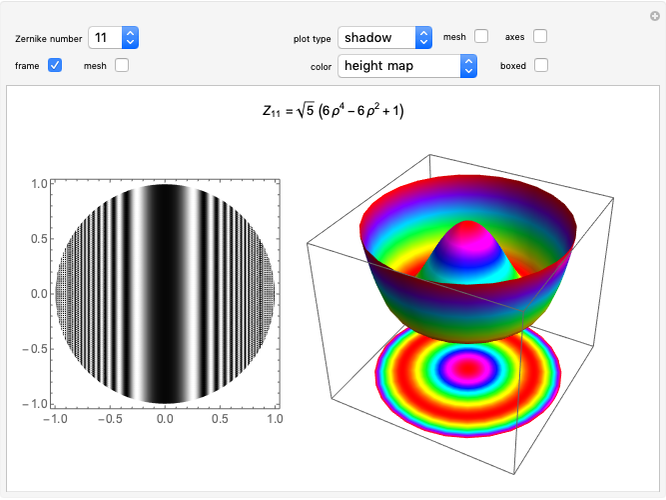
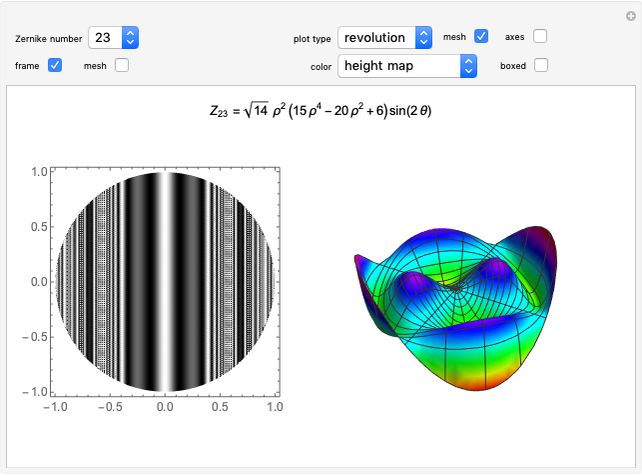
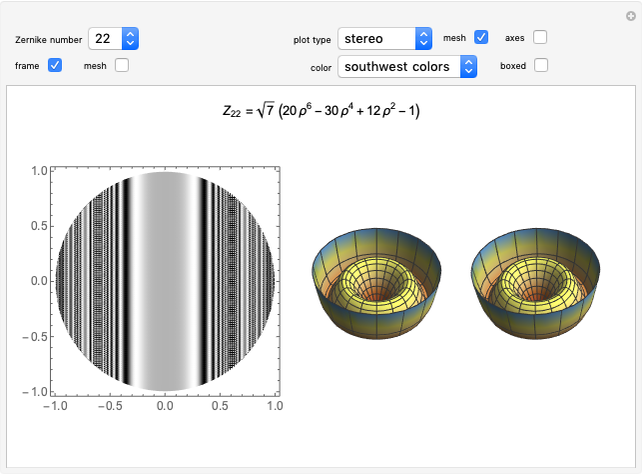
Plots of Zernike Polynomials

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
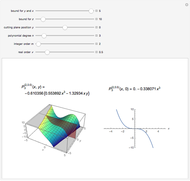
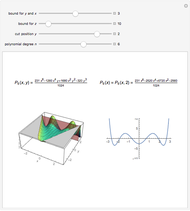
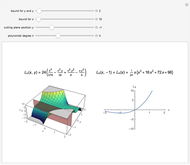
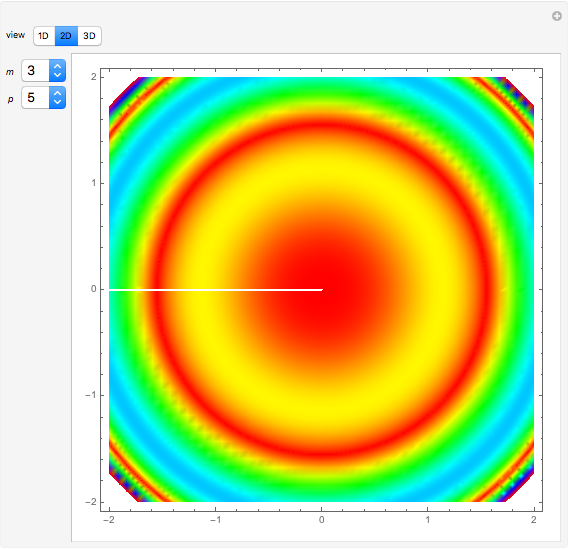
This Demonstration shows a 2D contour plot and a choice of 3D plots: a revolution plot, a shadow plot, stereo pairs of the revolution plots, or  and
and  profiles for various orthonormal Zernike circle polynomials
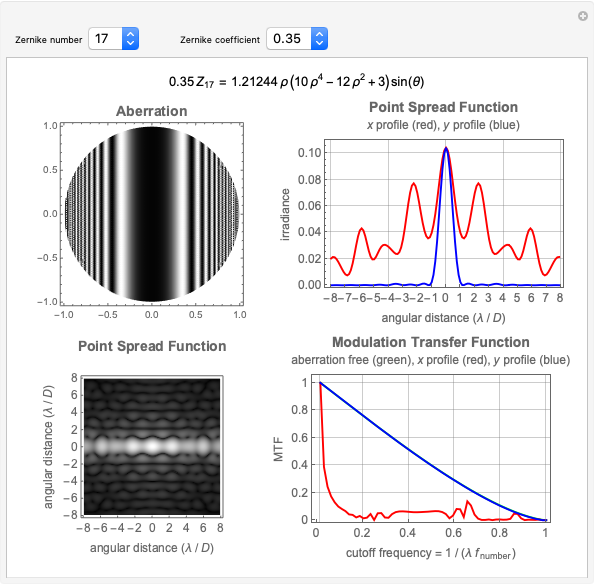
profiles for various orthonormal Zernike circle polynomials  . In the 3D plots, you can choose different color functions to show the height distribution of the functions. Zernike polynomials are commonly used to describe wavefront aberrations in optical systems.
. In the 3D plots, you can choose different color functions to show the height distribution of the functions. Zernike polynomials are commonly used to describe wavefront aberrations in optical systems.
Contributed by: James C. Wyant (January 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Wavefront aberrations are very important in studying the design, fabrication, and testing of all optical systems. Zernike polynomials, named after Nobel Prize winner Frits Zernike, are often used to describe these aberrations. The density plot shows what an interferogram testing an optical system with a given Zernike polynomial wavefront error would look like. The various 3D plots give a representation of the wavefront shape. A three-dimensional image of the wavefront aberration can be seen by looking at the stereo pairs of the 3D revolution plots. All the 3D plots can be rotated and zoomed.
References
[1] C-J. Kim and R. R. Shannon, "Catalog of Zernike Polynomials," in Applied Optics and Optical Engineering, Vol. X (R. R. Shannon and J. C. Wyant, eds.), San Diego: Academic Press, 1987 pp. 193–221.
[2] V. N. Mahajan, "Zernike Polynomial and Wavefront Fitting," in Optical Shop Testing (D. Malacara, ed.), 3rd ed., Hoboken, NJ: Wiley, 2007 pp. 498–546.
[3] V. N. Mahajan, Optical Imaging and Aberrations, Part II: Wave Diffraction Optics, Bellingham, WA: SPIE Press, 2001.
[4] J. C. Wyant and K. Creath, "Basic Wavefront Aberration Theory for Optical Metrology," in Applied Optics and Optical Engineering, Vol. XI (R. R. Shannon and J. C. Wyant, eds.), New York: Academic Press, 1992 pp. 11–53.
[5] J. C. Wyant. "webMathematica and LiveGraphics3D." (Jan 15, 2013) wyant.optics.arizona.edu/math.htm.
Permanent Citation