Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Products of Diagonal Lengths in the Regular Polygon

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

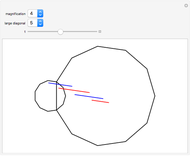
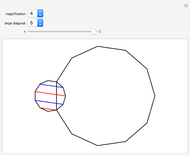
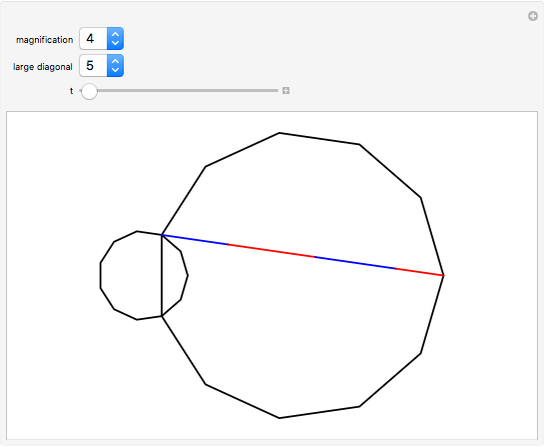
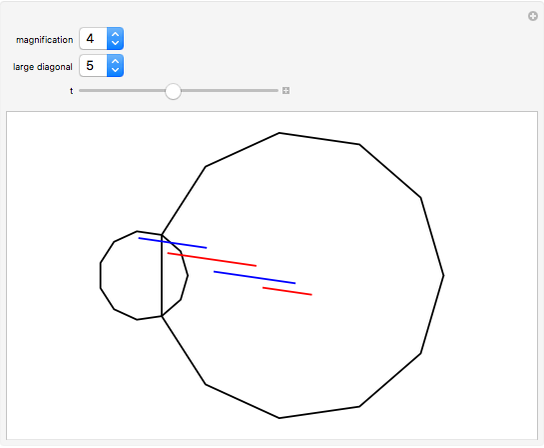
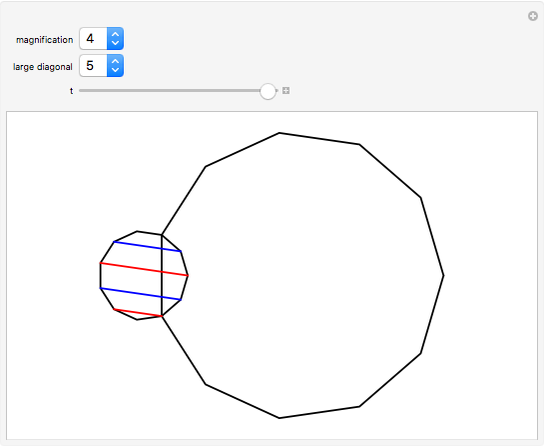
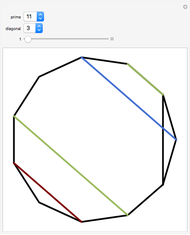
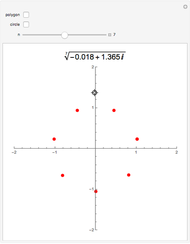
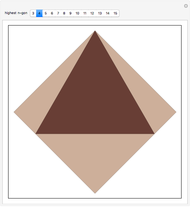
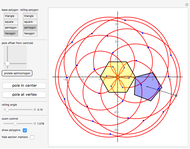
A regular polygon is scaled up in size so that its side length equals the length of some diagonal from the smaller polygon (the magnification diagonal). The diagonal lengths in the large polygon are seen to be sums of those in the smaller. The illustration is for an 11-gon.

[more]

The diagonals are numbered in order of increasing size. Choose a magnification diagonal and a diagonal from the larger polygon. Then move the slider to see the small diagonals involved in the sum.

[less]

Contributed by: Susan Hurley (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

If diagonal is scaled up using , then . The proof of this formula depends upon the fact that if , then the diagonal in a polygon of unit radius has length .

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send