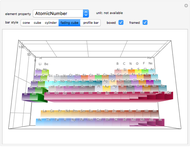
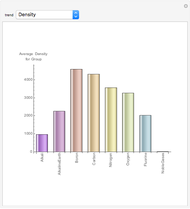
Mendeleev in his seminal work of 1869 demonstrated a relationship between the set of atomic weights and the natural numbers, thus implying that the properties of the chemical elements might have an underlying mathematical structure. The periodic system has since been much analyzed mathematically, using quantum physics, number theory, information theory, order theory, set theory and topology.
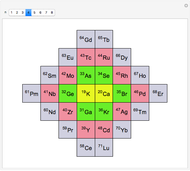
We demonstrate a variant of Charles Janet’s alternative periodic table, first proposed in 1928. Our mathematical approach can be called Pythagorean, since recurrent sequences are used to describe the periodic law, which can be represented by geometric constructions according to the Pythagorean concept of figurate numbers.
Expressed in such Pythagorean terms:
1. The length of any period is equal to twice the square of an integer; for example, 2, 2, 8, 8, 18, 18, 32, 32, ….
2. The length of any ( ) block of the table is equal to twice the uneven number, that is, a doubled gnomon of a square; for example,
) block of the table is equal to twice the uneven number, that is, a doubled gnomon of a square; for example,  .
3. Any dyad (in Janet's terms) ends with a tetrahedral number; for example, 4 Be, 20 Ca, 56 Ba, 220, 364, …. And this continues.
.
3. Any dyad (in Janet's terms) ends with a tetrahedral number; for example, 4 Be, 20 Ca, 56 Ba, 220, 364, …. And this continues.
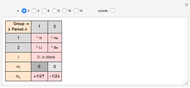
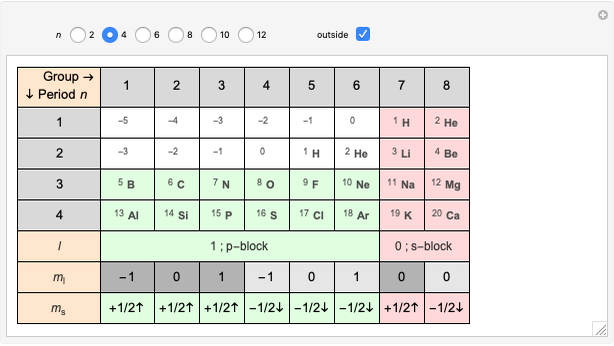
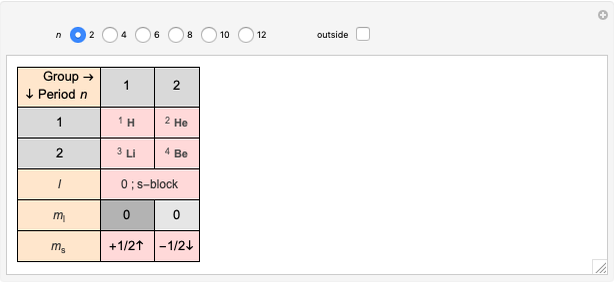
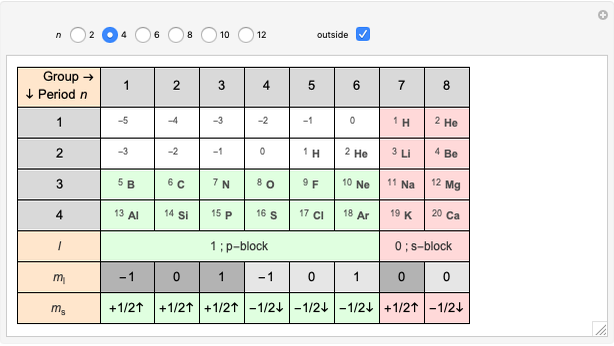
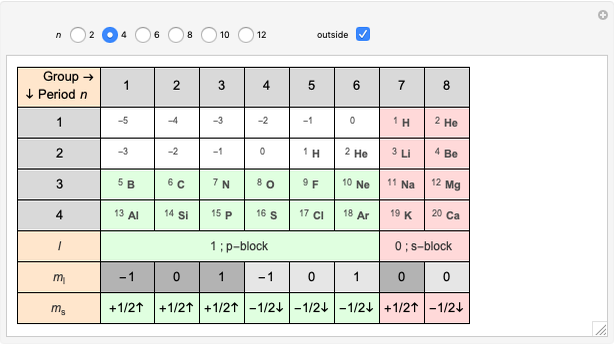
Janet's periodic table can be organized into rows representing electronic quantum numbers  and
and  . The table can be expanded to 12 periods and even continued beyond that. Note that the period numbering in Janet's table (correlated with the principal quantum number
. The table can be expanded to 12 periods and even continued beyond that. Note that the period numbering in Janet's table (correlated with the principal quantum number  ) differs from the conventional numbering. Also, this scheme does not reflect the few exceptions to the rules for filling outer electronic shells for some elements (e.g. Ni, Pd, Pt).
) differs from the conventional numbering. Also, this scheme does not reflect the few exceptions to the rules for filling outer electronic shells for some elements (e.g. Ni, Pd, Pt).
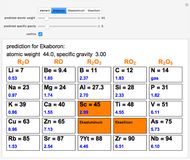
The cell values that appear in the "outside" cells are a byproduct of applying a mathematical formula and can be considered as food for thought.
[less]