Regular Tetrahedra Formed by Lattice Points Equidistant from the Origin
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
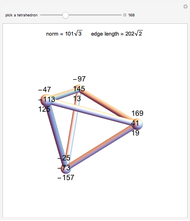
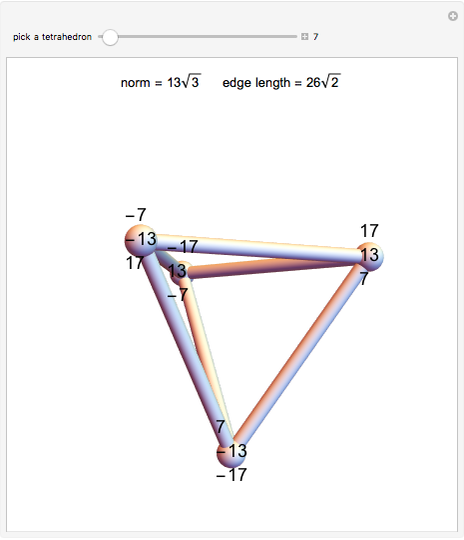
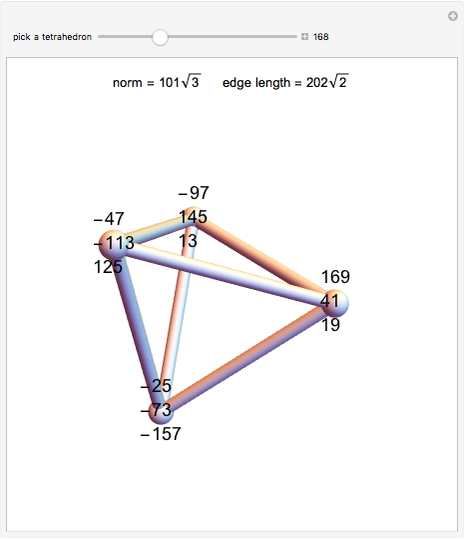
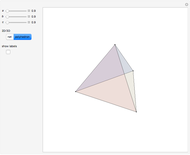
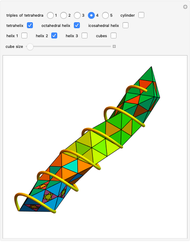
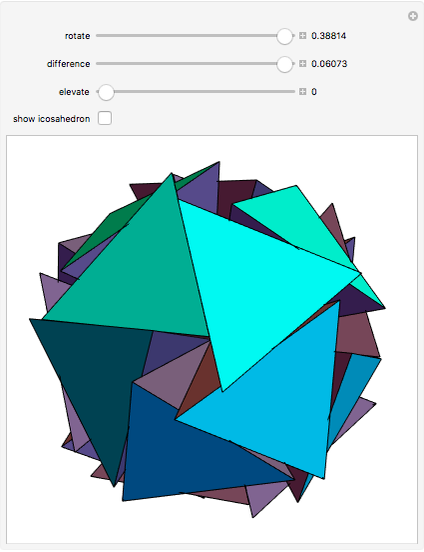
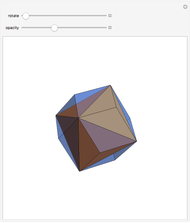
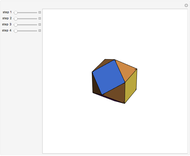
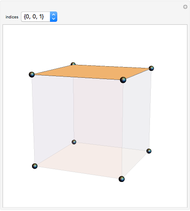
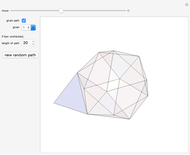
From an integer lattice, pick four points at the same distance from the origin (called the norm) that determine the vertices of a regular tetrahedron. Add the condition that the set of all 12 coordinates ( for each of the four vertices) does not have a common factor. Solutions we have found so far always appear to have a norm of the form
for each of the four vertices) does not have a common factor. Solutions we have found so far always appear to have a norm of the form  .
.
Contributed by: Ed Pegg Jr (January 2017)
Open content licensed under CC BY-NC-SA