Rhombic Triacosiohedron
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
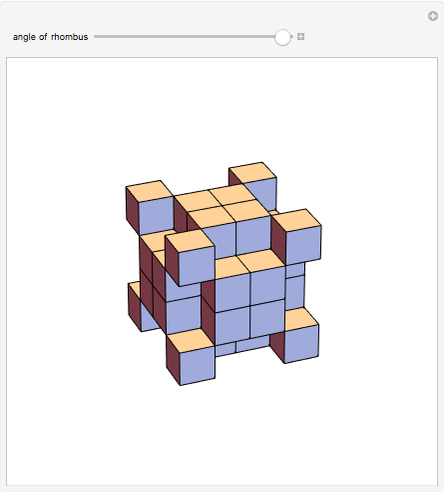
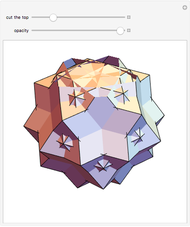
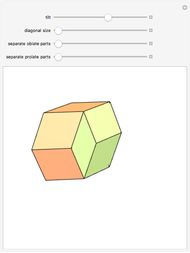
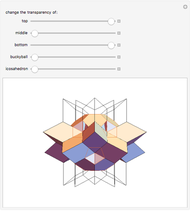
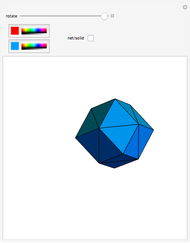
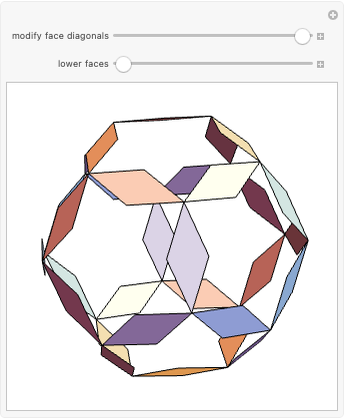
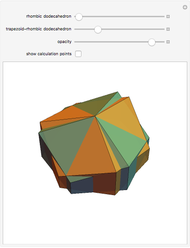
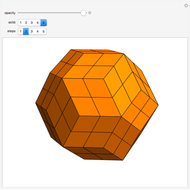
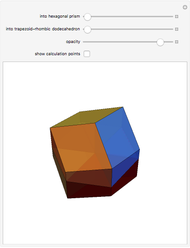
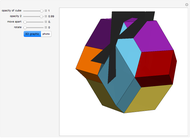
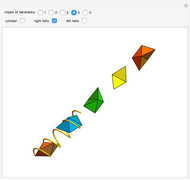
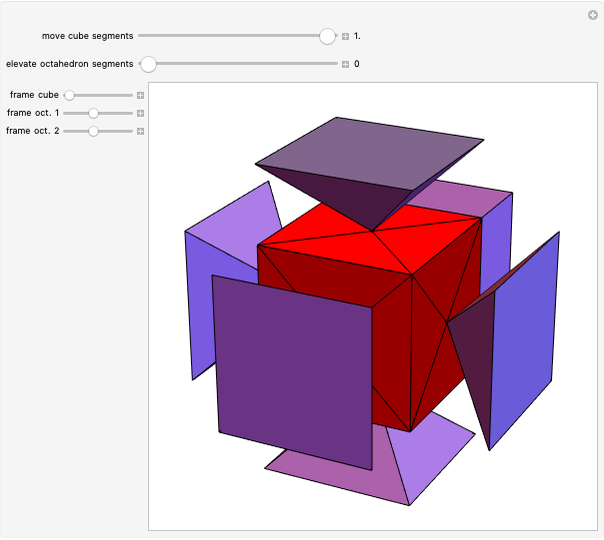
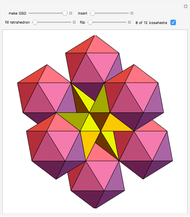
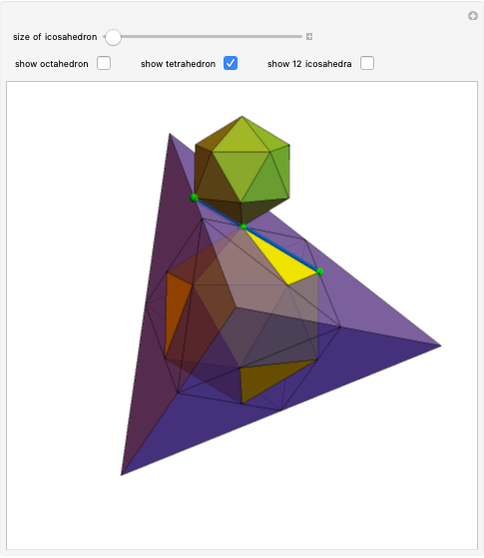
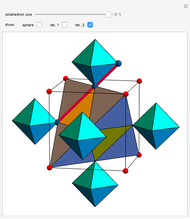
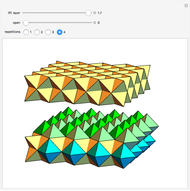
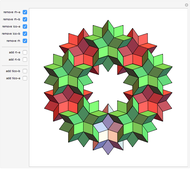
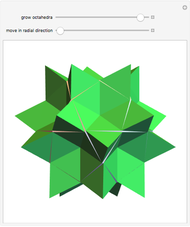
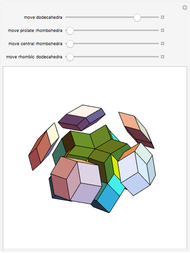
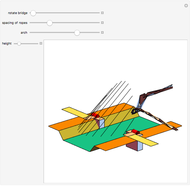
 congruent golden rhombi are aligned along the edges of a dodecahedron. The cluster produces a polyhedron with 280 vertices, 600 edges, and 300 congruent faces, each a rhombus the ratio of whose diagonals equals the golden ratio.
congruent golden rhombi are aligned along the edges of a dodecahedron. The cluster produces a polyhedron with 280 vertices, 600 edges, and 300 congruent faces, each a rhombus the ratio of whose diagonals equals the golden ratio.
Contributed by: Lajos Szilassi and Sándor Kabai (June 2008)
Additional contributions by: Gábor Gévay
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation