Rhombohedron with Variable Faces

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
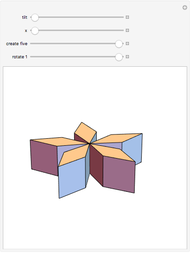
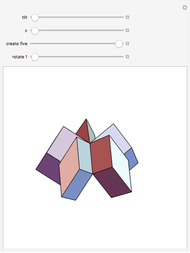
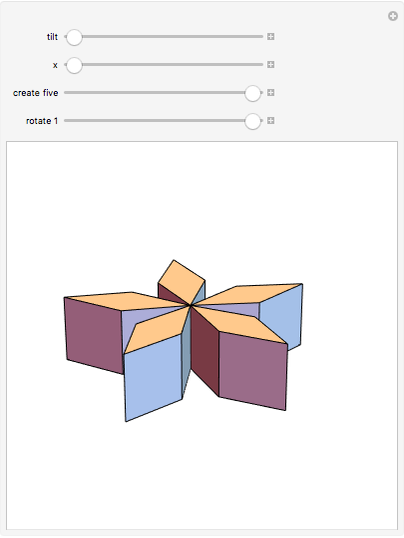
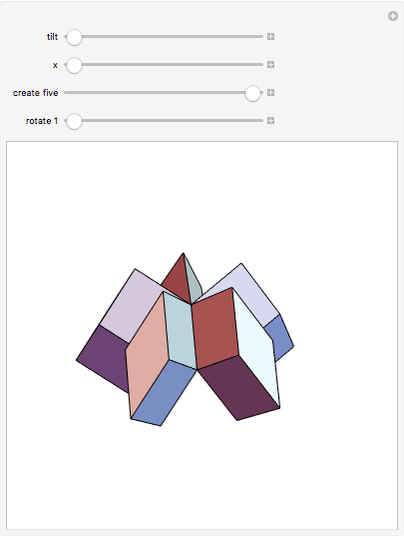
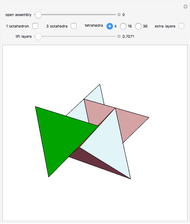
You can create various rhombohedra by tilting the four parallel edges of a cube or varying the face diagonals. This Demonstration focuses on the special case where the rhombohedron has four faces with diagonal ratio  and two faces with diagonal ratio
and two faces with diagonal ratio  , where
, where  is the golden ratio. Let the edge of a cube be
is the golden ratio. Let the edge of a cube be  . Tilt four parallel edges by
. Tilt four parallel edges by  degrees, then reduce the diagonal of two faces to
degrees, then reduce the diagonal of two faces to  . One interesting feature of this polyhedron is that the distance between the two thin rhombi is the golden ratio. The half-diagonals of the thin rhombus are
. One interesting feature of this polyhedron is that the distance between the two thin rhombi is the golden ratio. The half-diagonals of the thin rhombus are  and
and  . This illustrates an interesting relationship:
. This illustrates an interesting relationship:  , that is,
, that is,  .
.
Contributed by: Sándor Kabai (August 2008)
Open content licensed under CC BY-NC-SA
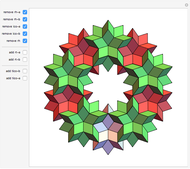
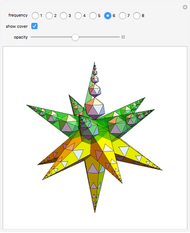
Snapshots
Details
This rhombohedron could be considered as a building block in structures where rhombi with diagonal ratios  or
or  occur. The rhombic enneacontahedron is an example of a
occur. The rhombic enneacontahedron is an example of a  rhombus and a
rhombus and a  rhombus; the rhombic dodecahedron is a
rhombus; the rhombic dodecahedron is a  rhombus and the median rhombic triacontahedron is a
rhombus and the median rhombic triacontahedron is a  rhombus.
rhombus.
Permanent Citation