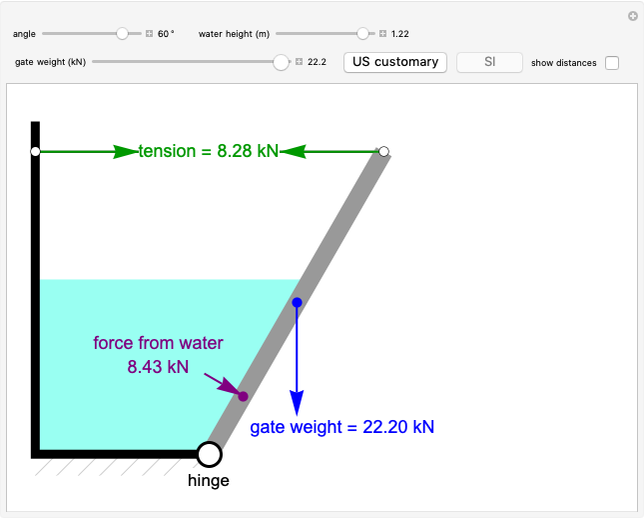
Seepage under a Dam by Flow Nets

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
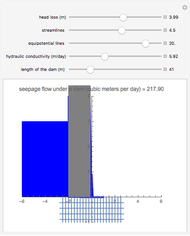
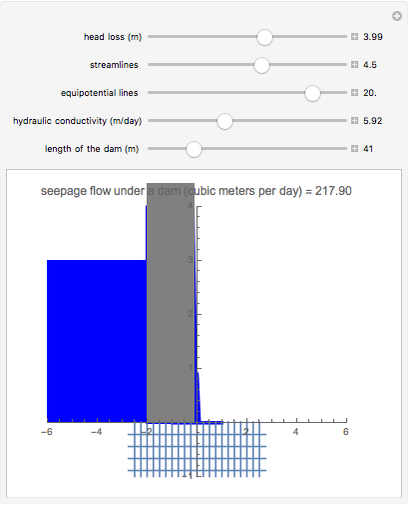
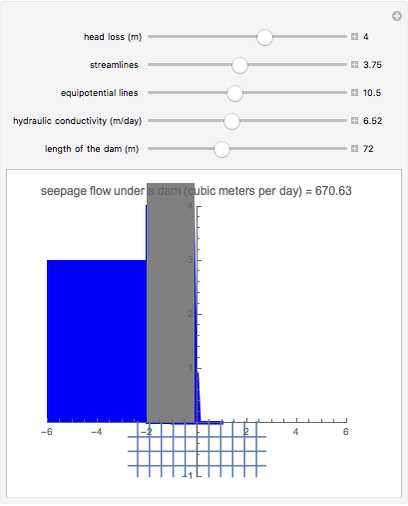
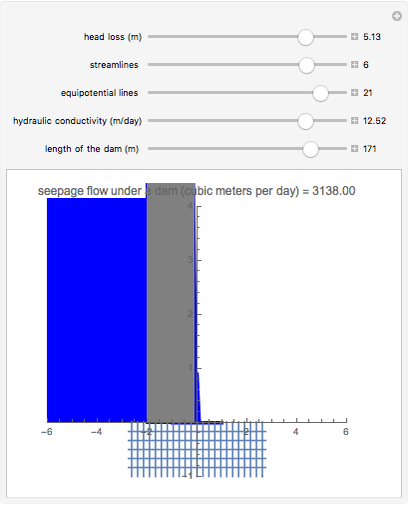
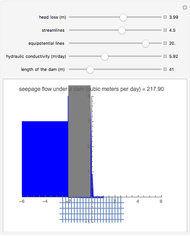
Given the elevation and the hydraulic conductivity under a dam, this Demonstration computes the discharge (per meter) that is perpendicular to the flow nets.
Contributed by: Leili Gordji and Sam Gordji (March 2011)
(University of Mississippi)
Open content licensed under CC BY-NC-SA
Snapshots
Details
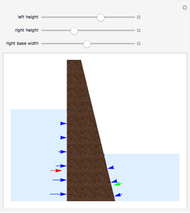
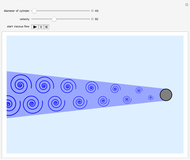
The rate of flow (or seepage)  of water under a dam is obtained by solving the equation of flow, which has the form of Laplace's equation. The analytical solution of Laplace's equation in Cartesian coordinates in two dimensions for a given set of boundary conditions results in two sets of solutions:
of water under a dam is obtained by solving the equation of flow, which has the form of Laplace's equation. The analytical solution of Laplace's equation in Cartesian coordinates in two dimensions for a given set of boundary conditions results in two sets of solutions:  , which represents the streamlines (or flow lines), and
, which represents the streamlines (or flow lines), and  , which represents the equipotentials. The equipotentials and streamlines are mutually orthogonal. The seepage may be calculated graphically [1]. The same results are obtained when these two equations are linearized and plotted to form a simple mesh of equal squares, as shown. Horizontal lines are streamlines where the water discharges from higher to lower elevations. When the graphical method is employed, there is seldom any need to have more than six or seven channels of streamlines. While each streamline carries the same flow, the equipotential lines are characterized by different values of the head. The equation for the flow nets is the special solution of Darcy's law. Vertical lines or equipotential lines represent potential differences in each channel. When equipotential lines are drawn, it is not usually necessary to draw more than 18 channels.
, which represents the equipotentials. The equipotentials and streamlines are mutually orthogonal. The seepage may be calculated graphically [1]. The same results are obtained when these two equations are linearized and plotted to form a simple mesh of equal squares, as shown. Horizontal lines are streamlines where the water discharges from higher to lower elevations. When the graphical method is employed, there is seldom any need to have more than six or seven channels of streamlines. While each streamline carries the same flow, the equipotential lines are characterized by different values of the head. The equation for the flow nets is the special solution of Darcy's law. Vertical lines or equipotential lines represent potential differences in each channel. When equipotential lines are drawn, it is not usually necessary to draw more than 18 channels.
References
[1] R. A. Freeze and J. A. Cherry, Ground Water, Englewood Cliffs, NJ: Prentice–Hall, 1979.
[2] P. B. Bedient, W. C. Huber, and B. E. Vieux, Hydrology and Floodplain Analysis, Englewood Cliffs, NJ: Prentice–Hall, 2007.
Permanent Citation
"Seepage under a Dam by Flow Nets"
http://demonstrations.wolfram.com/SeepageUnderADamByFlowNets/
Wolfram Demonstrations Project
Published: March 16 2011