Self-Replicating Graphs

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
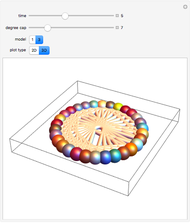
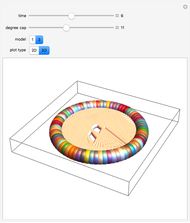
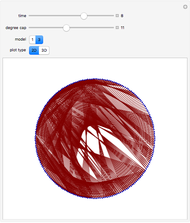
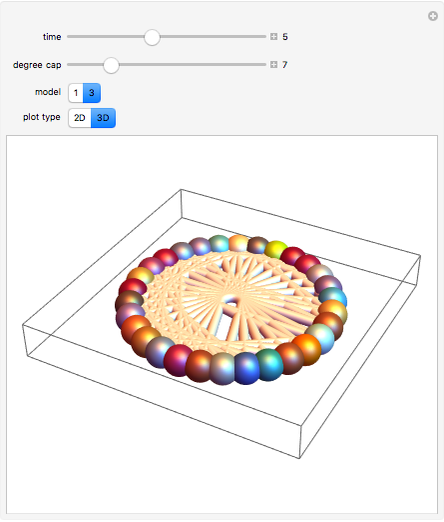
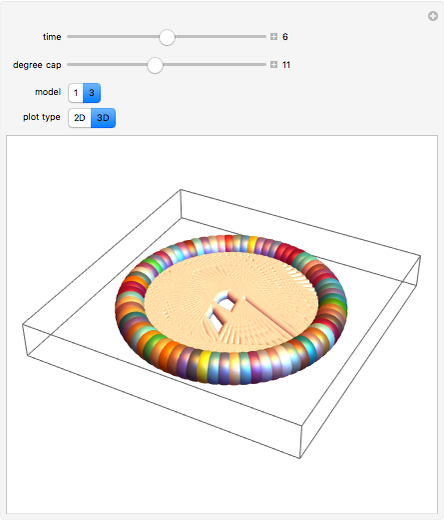
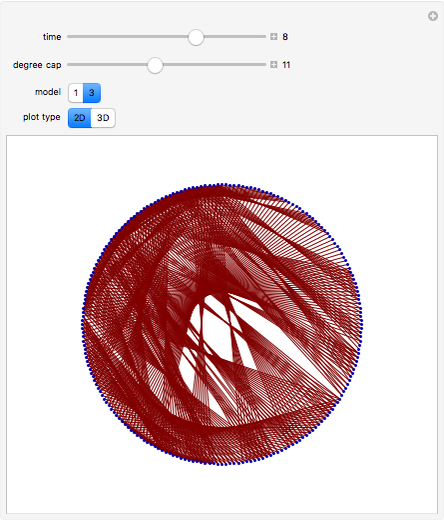
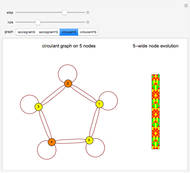
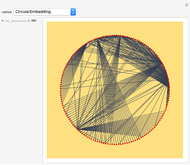
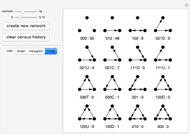
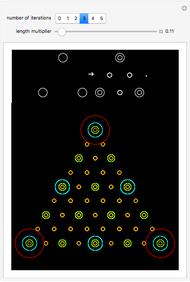
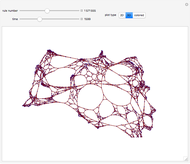
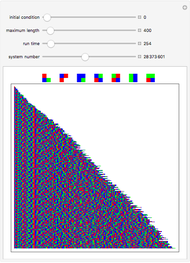
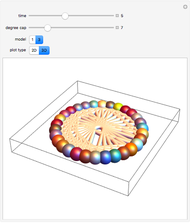
In these adaptive graph models, the vertices reproduce, while highly connected vertices die. Although the rules are simple, the models can generate highly complex behavior—a single edge can grow and break into thousands of different self-replicating structures. Every time step, the graph is updated by performing the "reproduction stage" and then the "killing stage". In the reproduction stage, every vertex has an "offspring vertex" that is born with the same connections as its parent. In the killing stage, every vertex with more connections than the "degree cap" gets destroyed. In model 1, offspring inherit their parent's neighborhood. In model 3, there is an extra "umbilical" connection between parent and offspring.
Contributed by: Richard Southwell (April 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The models are inspired by the growth of animal social networks. The reproduction stage is akin to springtime, when animals reproduce—having offspring with similar social relationships to their parents. The killing stage is akin to the winter time—when harsh conditions kill animals that share resources with too many neighbors. The rules behind the models are reminiscent of Conway's Game of Life, except these models generate their own space.
When the degree cap is large, the behavior can be highly complex. Consider model 1. When the degree cap is 4, a single edge grows (after three updates) to become a connected structure with 12 vertices. After another update, this structure breaks into four more edges, which continue self-replicating in the same way. When the degree cap is 10, a single edge eventually generates a vast "ecosystem" of 723 different structures that grow, change, and break into copies of one another. Some of the structures hold thousands of vertices. When the degree cap is infinite (i.e. pure reproduction, with no death), every bipartite graph will eventually appear as an induced subgraph of the resulting structure.
References
[1] R. Southwell and C. Cannings, "Some Models of Reproducing Graphs. III Game Based Reproduction," Applied Mathematics 1, 2010 pp. 334–342.
[2] R. Southwell and C. Cannings, "Games on Graphs That Grow Deterministically," GameNets, 2009 pp. 347–356.
Permanent Citation
"Self-Replicating Graphs"
http://demonstrations.wolfram.com/SelfReplicatingGraphs/
Wolfram Demonstrations Project
Published: April 11 2011