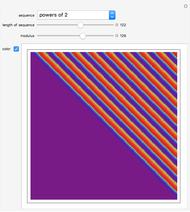
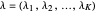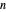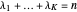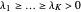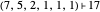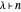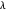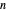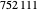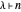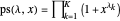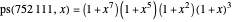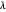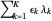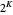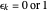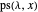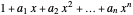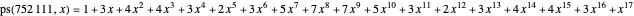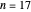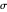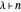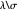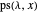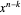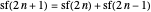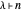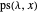Semi-Fibonacci Partitions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
This Demonstration counts the number of partition subsum polynomials without repeated roots.
[more]
Contributed by: George Beck (July 2019)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Definitions
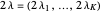
 ,
and if
,
and if 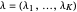 is a partition of
is a partition of 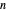 with one odd part, say
with one odd part, say  , define:
, define:  .
.
If 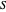 is a set of partitions, define
is a set of partitions, define 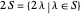 ,
, 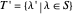 , and if
, and if 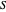 contains only partitions with one odd part,
contains only partitions with one odd part,  .
.
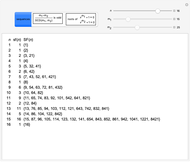
This defines the semi-Fibonacci partitions of 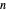 :
:
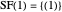 ,
,
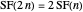 ,
,
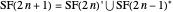 .
.
Then  ,
,  ,
, 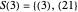 ,
, 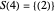 ,
,  , ….
, ….
Lemma 1
The roots of 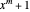 are
are 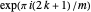 ,
, 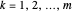 .
.
Proof
First check the roots: 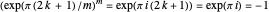 . Now check the roots are distinct: Suppose
. Now check the roots are distinct: Suppose 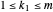 ,
, 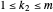 , and
, and 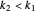 . Then
. Then 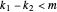 . Since
. Since 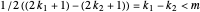 ,
, 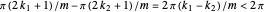 , so
, so 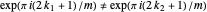 . Therefore the
. Therefore the 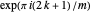 are distinct and are the
are distinct and are the 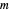 roots of
roots of  . \[FilledSquare]
. \[FilledSquare]
Lemma 2
The polynomials 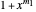 and
and 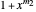 have a common root iff
have a common root iff 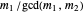 and
and 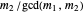 are both odd, in which case there are
are both odd, in which case there are 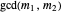 common roots. Therefore the polynomials have no common root iff
common roots. Therefore the polynomials have no common root iff 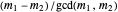 is odd.
is odd.
Proof
If the two polynomials have a common root, then there are integers 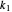 and
and 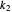 ,
, 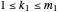 ,
, 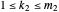 such that
such that 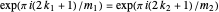 so
so  . Therefore
. Therefore 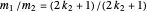 , which implies that the highest powers of 2 dividing
, which implies that the highest powers of 2 dividing 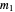 and
and 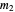 are equal, so that
are equal, so that 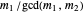 and
and 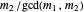 are both odd.
are both odd.
If  and
and  are both odd, let
are both odd, let 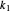 and
and 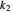 be such that
be such that 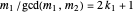 and
and 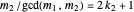 . Then
. Then 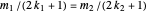 so
so 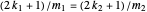 , which gives a common root of the two polynomials.
, which gives a common root of the two polynomials.
Suppose 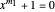 and
and 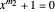 have a common root. Let
have a common root. Let 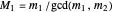 and
and  . Then the equations
. Then the equations 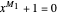 and
and 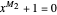 also have a common root, say
also have a common root, say 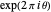 . Then with
. Then with 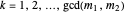 ,
, 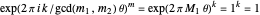 , so
, so  is also a solution of
is also a solution of 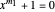 and likewise of
and likewise of 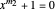 .
.
For the last statement, 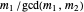 and
and 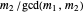 cannot both be even—the GCD would absorb the 2. So the polynomials have no common root iff one of
cannot both be even—the GCD would absorb the 2. So the polynomials have no common root iff one of 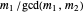 or
or 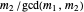 is odd and the other even, or, equivalently,
is odd and the other even, or, equivalently, 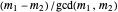 is odd. \[FilledSquare]
is odd. \[FilledSquare]
Lemma 3
The polynomial 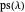 has no repeated root iff
has no repeated root iff  is odd for each pair of parts
is odd for each pair of parts 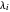 ,
, 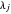 of
of 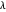 .
.
Proof
Apply lemma 2 to the definition 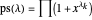 . \[FilledSquare]
. \[FilledSquare]
Lemma 4
If 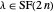 , then
, then 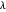 has only even parts.
If
has only even parts.
If 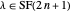 , then
, then  has exactly one odd part.
In the definition
has exactly one odd part.
In the definition 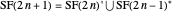 , the union is disjoint.
, the union is disjoint.
Proof
The parts of a partition in 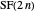 are clearly all even.
are clearly all even.
For induction, assume each partition in 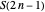 has at exactly one odd part; this is true for the base case
has at exactly one odd part; this is true for the base case 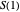 . Suppose
. Suppose 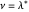 for some
for some 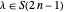 . Since
. Since 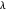 has at most one odd part, the same is true for
has at most one odd part, the same is true for  . Suppose
. Suppose 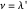 for some
for some 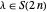 . Since
. Since  has no odd parts,
has no odd parts,  has exactly one odd part, namely 1.
has exactly one odd part, namely 1.
The union is disjoint because the odd parts of  are all 1 and the odd parts of
are all 1 and the odd parts of 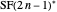 are all greater than 1. \[FilledSquare]
are all greater than 1. \[FilledSquare]
Lemma 5
 iff for each pair of parts
iff for each pair of parts 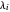 and
and 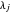 of
of  ,
,  is odd.
is odd.
Proof
This is vacuously true for the partitions with one part, 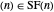 . For induction, assume the statement is true up to
. For induction, assume the statement is true up to 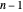 .
.
If 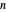 is even and
is even and 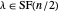 , then
, then 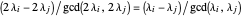 is odd by the induction hypothesis, so the condition holds for 2
is odd by the induction hypothesis, so the condition holds for 2 .
.
If 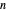 is odd and
is odd and 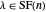 , either there is a
, either there is a 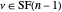 such that
such that 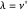 or there is a
or there is a  such that
such that 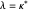 . In the first case, there is only one new part, 1; because
. In the first case, there is only one new part, 1; because 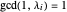 and all the other parts are even,
and all the other parts are even, 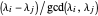 is odd. In the second case, by lemma 4,
is odd. In the second case, by lemma 4, 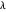 has exactly one odd part, so
has exactly one odd part, so 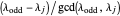 is odd and the others follow by induction, since the even parts belonged to partitions in
is odd and the others follow by induction, since the even parts belonged to partitions in 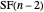 . \[FilledSquare]
. \[FilledSquare]
Lemma 6
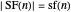 .
.
Proof
For induction, the base case 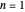 is
is 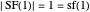 . By definition of
. By definition of  ,
,  . By lemma 4, since the union is disjoint,
. By lemma 4, since the union is disjoint, 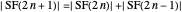 . Therefore
. Therefore 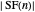 satisfies the same conditions as
satisfies the same conditions as 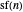 and they are the same sequence. \[FilledSquare]
and they are the same sequence. \[FilledSquare]
Theorem
The number of partitions  for which
for which 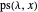 has no repeated root is the semi-Fibonacci sequence.
has no repeated root is the semi-Fibonacci sequence.
Proof
By lemma 3,  has no repeated root iff
has no repeated root iff 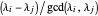 is odd for each pair of parts
is odd for each pair of parts  ,
, 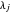 of
of  . By lemma 5, the latter statement is equivalent to
. By lemma 5, the latter statement is equivalent to 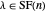 . By lemma 6, the number of
. By lemma 6, the number of  with no repeated root is counted by
with no repeated root is counted by 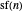 . \[FilledSquare]
. \[FilledSquare]
References
[1] N. J. A. Sloane "A000009." The On-Line Encyclopedia of Integer Sequences. https://oeis.org/A000009.
[2] N. J. A. Sloane "A126796." The On-Line Encyclopedia of Integer Sequences. https://oeis.org/A126796.
[3] N. J. A. Sloane "A030067." The On-Line Encyclopedia of Integer Sequences. https://oeis.org/A030067.
Permanent Citation