Fibonacci Numbers and the Golden Ratio
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
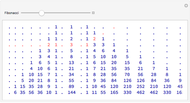
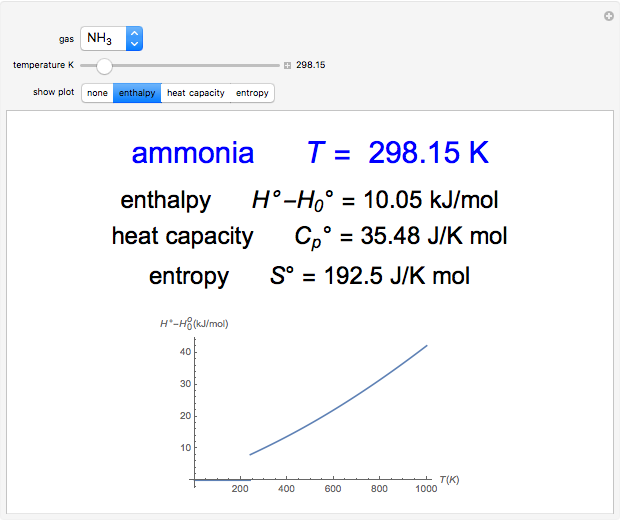
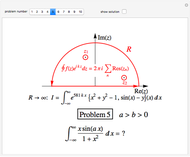
The sequence of Fibonacci numbers is given by 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, …, in which each number is the sum of the two preceding numbers. This can be expressed as  with
with  and
and  .
.
Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
S. M. Blinder, Guide to Essential Math, Amsterdam: Elsevier, 2008 pp. 7–8.
Permanent Citation