Sledding on a Bumpy Slope: Chaos and Strange Attractor

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
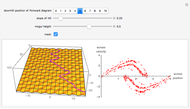
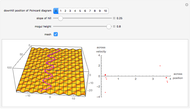
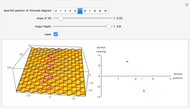
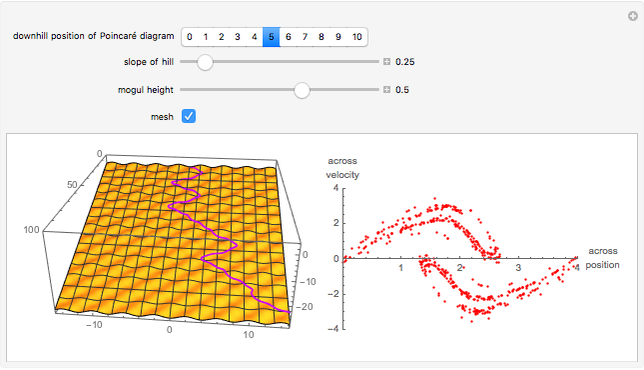
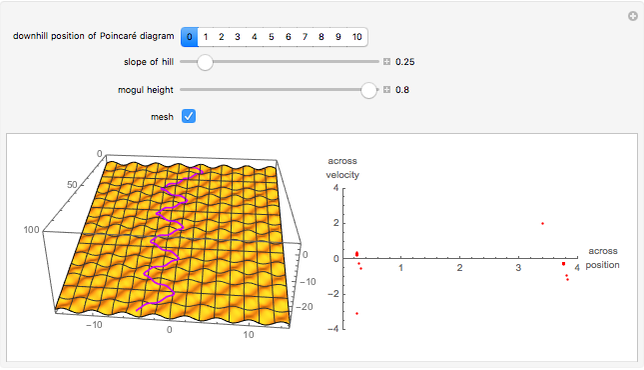
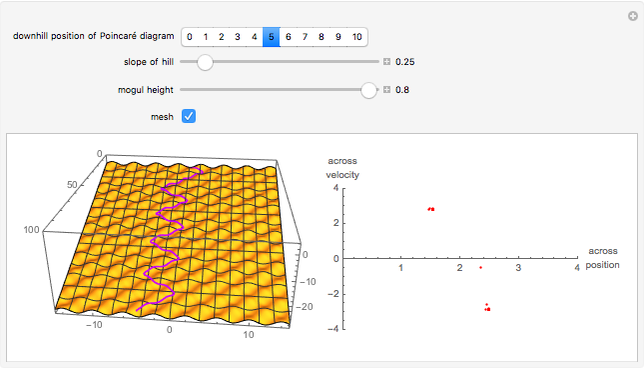
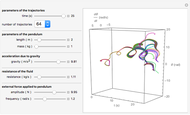
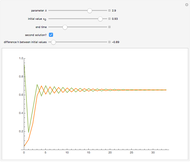
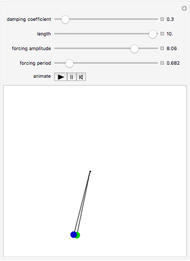
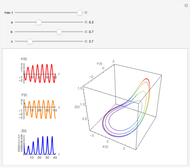
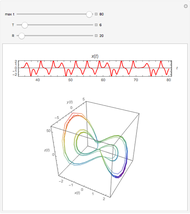
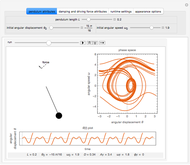
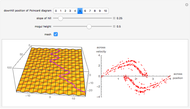
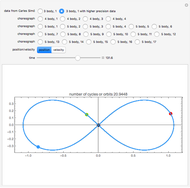
This Demonstration shows a sled sliding down a mogul-covered hill. The mogul pattern is periodic: 10 meters long downhill by 5 meters wide across the hill. The accompanying Poincaré diagram shows the range of points of cross-hill velocity versus position as the sled proceeds downhill. The points for the Poincaré diagram are taken at 10-meter downhill intervals; you can vary this position within the 10-meter range of the repetitive pattern. In chaotic paths, the Poincaré pattern shows a limited range of values, and even more so in a nonchaotic path.
Contributed by: Robert M. Lurie (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
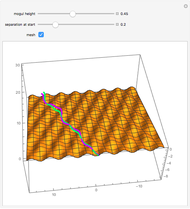
In the three snapshots, the sled follows a path down the hill with small moguls (0.5 in Thumbnail and Snapshot 1) with the Poincaré plot at a different downhill position (0 and 5) that form "strange attractors". On the hill with very large moguls (0.8 in Snapshot 2 and 3) the path is almost nonchaotic since the repeated cross-hill velocity and positions of the sled are very close to constant values.
For an excellent discussion of chaos, strange attractors, and other aspects of chaos, see E. N. Lorenz, The Essence of Chaos, Seattle: University of Washington Press, 1993; paperback, 1995. Of course, the icon of chaos was developed by Dr. Lorenz. The implementation of the sliding board by the author is found in R. M. Lurie, "A Review and Demonstration of 'The Essence of Chaos' by Edward N. Lorenz," Mathematica for Education and Research, 11(4), 2006 pp. 404–425, updated for Mathematica 7 here.
Permanent Citation
"Sledding on a Bumpy Slope: Chaos and Strange Attractor"
http://demonstrations.wolfram.com/SleddingOnABumpySlopeChaosAndStrangeAttractor/
Wolfram Demonstrations Project
Published: March 7 2011