Space-Filling Polyhedra Based on a Truncated Octahedron

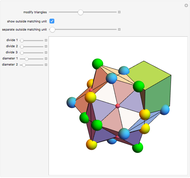
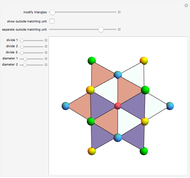
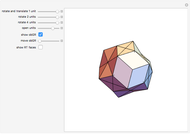
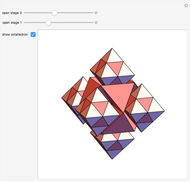
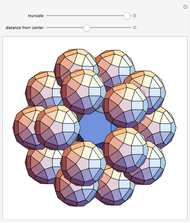
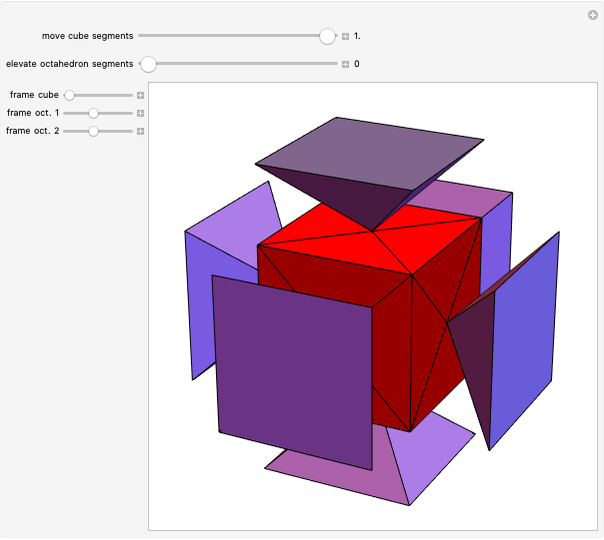
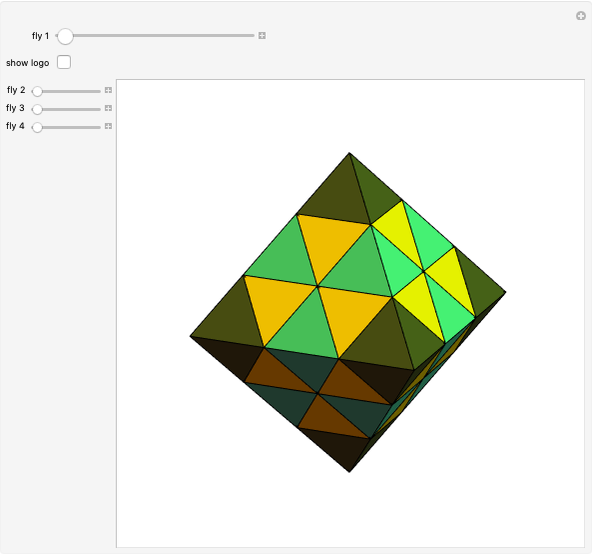
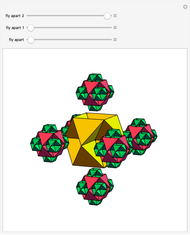
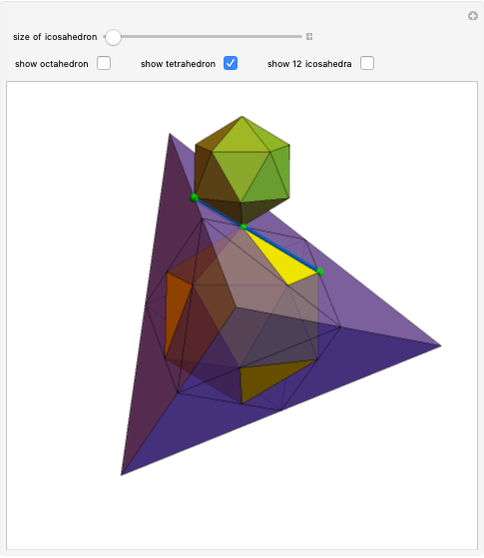
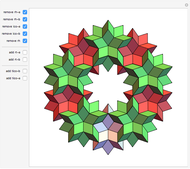
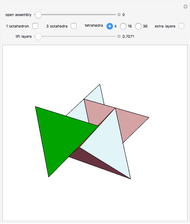
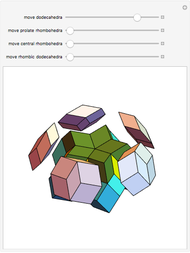
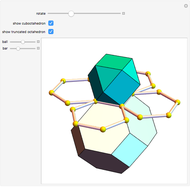
Each hexagonal face of a truncated octahedron is divided into six triangles. The triangles can be modified by moving their vertices along the edges of a cube. When the vertices of the triangles reach the vertices of the cube, the polyhedra becomes an Escher's solid (one of the three stellations of the rhombic dodecahedron). Between the truncated octahedron and the Escher's solid an infinite number of 54-faced space-filling polyhedra are produced, with the one matching the rhombic triacontahedron among them.