Statistical Mechanics of Money

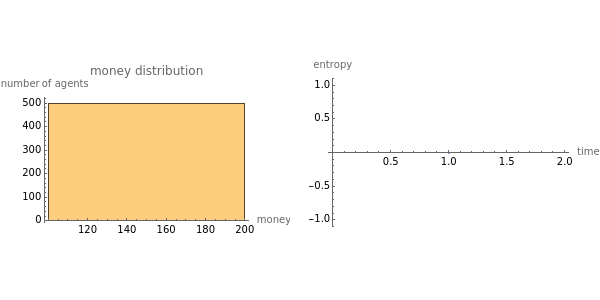
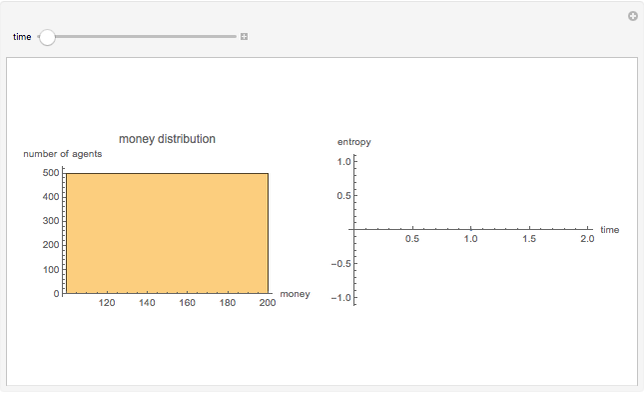
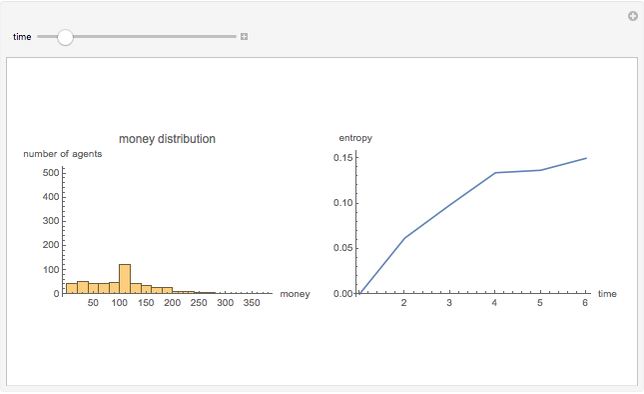
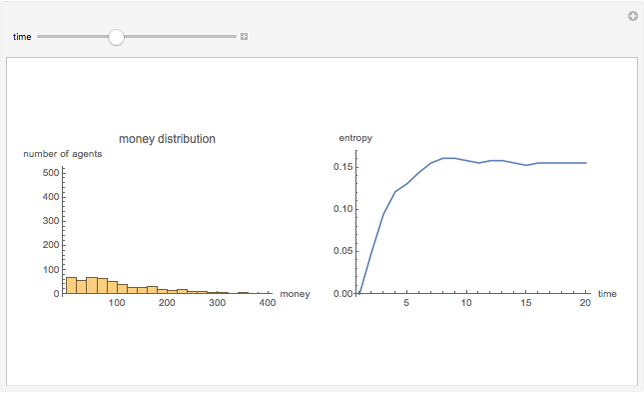
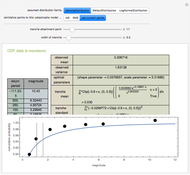
The empirical distribution of the majority of people's wealth is consistent with an exponential (Boltzmann-Gibbs) distribution. This outcome can be replicated by an abstract agent-based simulation that models the exchange of money for goods in market economies. In this simulation, (i) total money is conserved and (ii) a random amount of money is transferred from one randomly selected agent to another ad infinitum. The first plot tracks the instantaneous money distribution (a simple proxy for wealth). The money distribution is initially equitable but rapidly converges to the highly unequal exponential distribution, at which point the economy enters statistical equilibrium. The second plot tracks the entropy of the money distribution, which increases to a maximum. The exponential distribution is the maximum entropy distribution under the constraint of money conservation. So market exchange between large numbers of independent agents is a mechanism that produces the "most disorderly" distribution of wealth subject to a simple conservation constraint.